
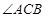 的平分线交AE于点F,交AB于D点.
的平分线交AE于点F,交AB于D点.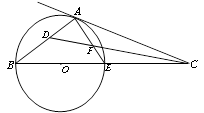
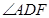 的度数;
的度数; ;(2)
;(2) 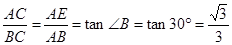
 AC为圆O的切线,∴
AC为圆O的切线,∴ 又知,DC是
又知,DC是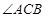 的平分线,
的平分线, ∴
∴
 又因为BE为圆O的直径, ∴
又因为BE为圆O的直径, ∴


 ,
, ,∴
,∴ ∽
∽ ∴
∴
 AB="AC," ∴
AB="AC," ∴ ,
,


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:不详 题型:解答题
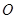 的半径OB垂直于直径AC,
的半径OB垂直于直径AC,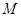 为AO上一点,
为AO上一点, 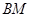 的延长线交⊙
的延长线交⊙ 于点N,过点N的切线交CA的延长线于点P.
于点N,过点N的切线交CA的延长线于点P.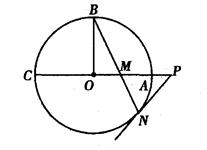
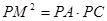 ;
; 的半径为
的半径为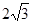 ,OA=
,OA=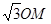 ,求
,求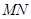 的长.
的长.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
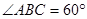 ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
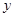 轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.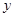 轴正半轴上时,求边BC在旋转过程中所扫过的面积;
轴正半轴上时,求边BC在旋转过程中所扫过的面积;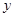 轴的交点为M(如图2),线段BC与直线
轴的交点为M(如图2),线段BC与直线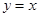 的交点为N.设
的交点为N.设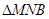 的周长为
的周长为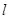 ,在正方形OABC旋转的过程中
,在正方形OABC旋转的过程中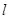 值是否有改变?并说明你的结论;
值是否有改变?并说明你的结论;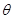 ,当
,当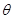 为何值时,
为何值时,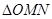 的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.
的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.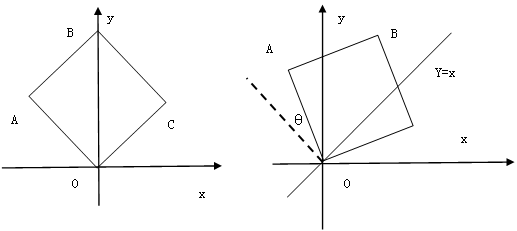

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com