
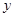 轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.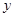 轴正半轴上时,求边BC在旋转过程中所扫过的面积;
轴正半轴上时,求边BC在旋转过程中所扫过的面积;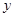 轴的交点为M(如图2),线段BC与直线
轴的交点为M(如图2),线段BC与直线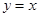 的交点为N.设
的交点为N.设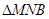 的周长为
的周长为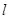 ,在正方形OABC旋转的过程中
,在正方形OABC旋转的过程中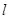 值是否有改变?并说明你的结论;
值是否有改变?并说明你的结论;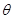 ,当
,当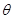 为何值时,
为何值时,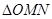 的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.
的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.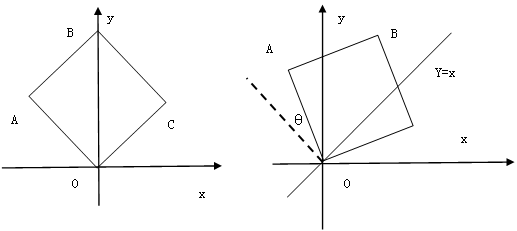

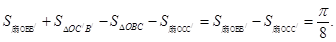
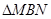 的周长为定值2. (3)
的周长为定值2. (3)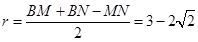 .
.  ,再利用S=S扇形OBB′+S△OC′B′-S△OCB-S扇形OCC′=S扇形OBB′-S扇形OCC′求出即可;
,再利用S=S扇形OBB′+S△OC′B′-S△OCB-S扇形OCC′=S扇形OBB′-S扇形OCC′求出即可;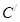 、B在
、B在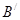 、A在
、A在 .
.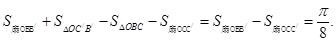 ………….4分
………….4分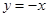 于E点,在
于E点,在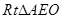 与
与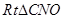 中,
中,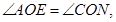
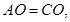 所以
所以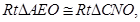 所以
所以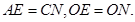
 所以
所以
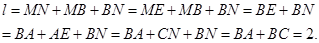 故
故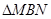 的周长为定值2.…..10分
的周长为定值2.…..10分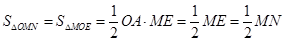 ,
,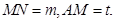 由(2)知,在
由(2)知,在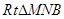 中,
中,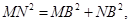
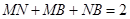 ,所以
,所以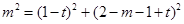 ,得:
,得: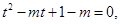
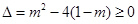 ,所以
,所以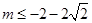 (舍去)或
(舍去)或
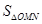 的最小值为
的最小值为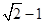 . …….13分
. …….13分
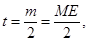 ∴A为ME的中点.
∴A为ME的中点.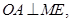 所以OA是
所以OA是 的平分线,
的平分线,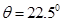 . ……15分
. ……15分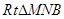 中,
中,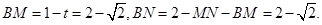 设
设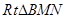 的内切圆半径为r,所以
的内切圆半径为r,所以 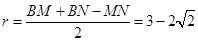 . ……18分
. ……18分

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
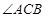 的平分线交AE于点F,交AB于D点.
的平分线交AE于点F,交AB于D点.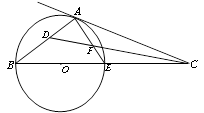
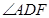 的度数;
的度数;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com