
【题目】已知由n(n∈N*)个正整数构成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),记SA=a1+a2+…+an,对于任意不大于SA的正整数m,均存在集合A的一个子集,使得该子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求证:“a1,a2,…,an成等差数列”的充要条件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值时an的最大值.
【答案】(1)a1=1,a2=2;(2)证明见解析;(3)n最小值为11,an的最大值1010
【解析】
(1)考虑元素1,2,结合新定义SA,可得所求值;
(2)从两个方面证明,结合等差数列的性质和求和公式,即可得证;
(3)由于含有n个元素的非空子集个数有2n﹣1,讨论当n=10时,n=11时,结合条件和新定义,推理可得所求.
(1)由条件知1≤SA,必有1∈A,又a1<a2<…<an均为整数,a1=1,
2≤SA,由SA的定义及a1<a2<…<an均为整数,必有2∈A,a2=2;
(2)证明:必要性:由“a1,a2,…,an成等差数列”及a1=1,a2=2,
得ai=i(i=1,2,…,n)此时A={1,2,3,…,n}满足题目要求,
从而![]() ;
;
充分性:由条件知a1<a2<…<an,且均为正整数,可得ai≥i(i=1,2,3,…,n),
故![]() ,当且仅当ai=i(i=1,2,3,…,n)时,上式等号成立.
,当且仅当ai=i(i=1,2,3,…,n)时,上式等号成立.
于是当![]() 时,ai=i(i=1,2,3,…,n),从而a1,a2,…,an成等差数列.
时,ai=i(i=1,2,3,…,n),从而a1,a2,…,an成等差数列.
所以“a1,a2,…,an成等差数列”的充要条件是“![]() ”;
”;
(Ⅲ)由于含有n个元素的非空子集个数有2n-1,故当n=10时,210﹣1=1023,
此时A的非空子集的元素之和最多表示1023个不同的整数m,不符合要求.
而用11个元素的集合A={1,2,4,8,16,32,64,128,256,512,1024}的非空子集的元素之和
可以表示1,2,3,…,2046,2047共2047个正整数.
因此当SA=2020时,n的最小值为11.
记S10=a1+a2+…+a10,则S10+a11=2020并且S10+1≥a11.
事实上若S10+1<a11,2020=S10+a11<2a11,则a11>1010,S10<a11<1010,
所以m=1010时无法用集合A的非空子集的元素之和表示,与题意不符.
于是2020=S10+a11≥2a11﹣1,得![]() ,
,![]() ,所以a11≤1010.
,所以a11≤1010.
当a11=1010时,A={1,2,4,8,16,32,64,128,256,499,1010}满足题意,
所以当SA=2020时,n的最小值为11,此时an的最大值1010.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】现有四个函数①y=x|sinx|,②y=xcos|x|,③![]() ,④y=xln|x|的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
,④y=xln|x|的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
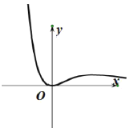
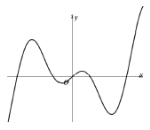
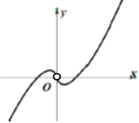
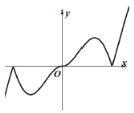
A.①④②③B.①④③②C.③②④①D.③④②①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌赛马是《史记》中记载的一个故事,说的是齐国大将军田忌经常与齐国众公子赛马,孙膑发现田忌的马和其他人的马相差并不远,都分为上、中、下三等.于是孙膑给田忌将军献策:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得了许多赌注.假设田忌的各等级马与某公子的各等级马进行一场比赛,田忌获胜的概率如下表所示:
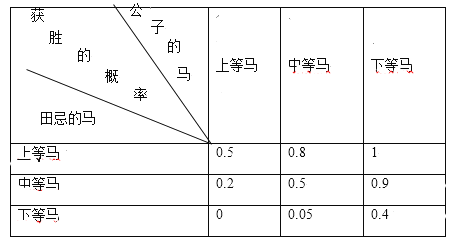
比赛规则规定:一次比赛由三场赛马组成,每场由公子和田忌各出一匹马参赛,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
(1)如果按孙膑的策略比赛一次,求田忌获胜的概率;
(2)如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ).
).
(Ⅰ)若![]() 是函数
是函数![]() 的一个极值点,求
的一个极值点,求![]() 的值;
的值;
(Ⅱ)求证:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅲ)若对任意的![]() (1,2),总存在
(1,2),总存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取范围.
的取范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() ,其右焦点
,其右焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 且垂直于抛物线对称轴的直线与椭圆交于
且垂直于抛物线对称轴的直线与椭圆交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.
两点.![]()
(1)求椭圆的方程;
(2)若直线l与(1)中椭圆相交于![]() ,
,![]() 两点, 直线
两点, 直线![]() ,
, ![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() (其中
(其中![]() ),且
),且![]() ,
,![]() ,
,![]() 成等比数列;设
成等比数列;设![]() 的面积为
的面积为![]() , 以
, 以![]() 、
、![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,
, ![]() , 求
, 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() (任意项都不为零)的前
(任意项都不为零)的前![]() 项和为
项和为![]() ,首项为
,首项为![]() ,对于任意
,对于任意![]() ,满足
,满足![]() .
.
(1)数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() 使得
使得![]() 成等比数列,且
成等比数列,且![]() 成等差数列?若存在,试求
成等差数列?若存在,试求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设数列![]() ,
, ,若由
,若由![]() 的前
的前![]() 项依次构成的数列是单调递增数列,求正整数
项依次构成的数列是单调递增数列,求正整数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com