
【题目】已知椭圆方程为![]() ,其右焦点
,其右焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 且垂直于抛物线对称轴的直线与椭圆交于
且垂直于抛物线对称轴的直线与椭圆交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.
两点.![]()
(1)求椭圆的方程;
(2)若直线l与(1)中椭圆相交于![]() ,
,![]() 两点, 直线
两点, 直线![]() ,
, ![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() (其中
(其中![]() ),且
),且![]() ,
,![]() ,
,![]() 成等比数列;设
成等比数列;设![]() 的面积为
的面积为![]() , 以
, 以![]() 、
、![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,
, ![]() , 求
, 求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意可得![]() ,
,![]() ,即得
,即得![]() ,结合
,结合![]() 可得椭圆方程;(2)设直线
可得椭圆方程;(2)设直线![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立,写出韦达定理,由
,将直线方程与椭圆方程联立,写出韦达定理,由![]() ,
,![]() ,
,![]() 成等比数列,可解得k值,然后分别求出S,
成等比数列,可解得k值,然后分别求出S,![]() ,写出
,写出![]() 的表达式,利用基本不等式可得取值范围.
的表达式,利用基本不等式可得取值范围.
(1)由抛物线方程得![]() ,椭圆方程为
,椭圆方程为![]() ,过F垂直于抛物线对称轴的直线与椭圆交于M,N两点,可得
,过F垂直于抛物线对称轴的直线与椭圆交于M,N两点,可得![]() ,与抛物线交于C,D两点可得
,与抛物线交于C,D两点可得![]() ,
, 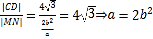 ,
, ![]() ,
,![]()
![]() ,
,
所以椭圆方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由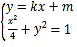 可得
可得![]() ,
,
由韦达定理: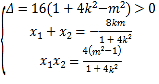 ,
,
∵![]() ,
,![]() ,
,![]() 构成等比数列,
构成等比数列,![]()
![]() ,
,
即![]()
由韦达定理代入化简得:![]() ,∵
,∵ ![]() ,
,![]()
![]() .
.
此时![]() ,即
,即![]() .
.
又由![]() 三点不共线得
三点不共线得![]() ,从而
,从而![]() .
.
故![]()
![]()
∵![]() ,
,![]() ,
,![]() ,
,
则![]()
![]() 为定值.
为定值.
![]()
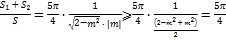 ,
,
当且仅当![]() 即
即![]() 时等号成立.
时等号成立.
综上:![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
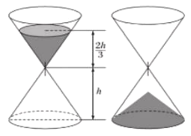
【题目】沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).假设该沙漏每秒钟漏下
(细管长度忽略不计).假设该沙漏每秒钟漏下![]() 的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是( )
的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是( )
A.沙漏中的细沙体积为![]()
B.沙漏的体积是![]()
C.细沙全部漏入下部后此锥形沙堆的高度约为2.4cm
D.该沙漏的一个沙时大约是1985秒(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由n(n∈N*)个正整数构成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),记SA=a1+a2+…+an,对于任意不大于SA的正整数m,均存在集合A的一个子集,使得该子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求证:“a1,a2,…,an成等差数列”的充要条件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值时an的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业参加![]() 项目生产的工人为
项目生产的工人为![]() 人,平均每人每年创造利润
人,平均每人每年创造利润![]() 万元.根据现实的需要,从
万元.根据现实的需要,从![]() 项目中调出
项目中调出![]() 人参与
人参与![]() 项目的售后服务工作,每人每年可以创造利润
项目的售后服务工作,每人每年可以创造利润![]() 万元(
万元(![]() ),
),![]() 项目余下的工人每人每年创造利图需要提高
项目余下的工人每人每年创造利图需要提高![]()
(1)若要保证![]() 项目余下的工人创造的年总利润不低于原来
项目余下的工人创造的年总利润不低于原来![]() 名工人创造的年总利润,则最多调出多少人参加
名工人创造的年总利润,则最多调出多少人参加![]() 项目从事售后服务工作?
项目从事售后服务工作?
(2)在(1)的条件下,当从![]() 项目调出的人数不能超过总人数的
项目调出的人数不能超过总人数的![]() 时,才能使得
时,才能使得![]() 项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数
项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,数列
,数列![]() 满足
满足![]() .
.
![]() Ⅰ
Ⅰ![]() 求数列
求数列![]() 和数列
和数列![]() 的通项公式;
的通项公式;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,若
,若![]() 对于一切的正整数
对于一切的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
![]() Ⅲ
Ⅲ![]() 数列
数列![]() 中是否存在
中是否存在![]() ,且
,且 ![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据国家统计局发布的数据,2019年11月全国![]() (居民消费价格指数),同比上涨
(居民消费价格指数),同比上涨![]() ,
,![]() 上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响
上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响![]() 上涨3.27个百分点.下图是2019年11月
上涨3.27个百分点.下图是2019年11月![]() 一篮子商品权重,根据该图,下列四个结论正确的有______.
一篮子商品权重,根据该图,下列四个结论正确的有______.
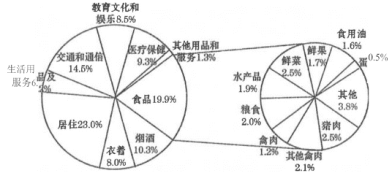
①![]() 一篮子商品中权重最大的是居住
一篮子商品中权重最大的是居住
②![]() 一篮子商品中吃穿住所占权重超过
一篮子商品中吃穿住所占权重超过![]()
③猪肉在![]() 一篮子商品中权重为
一篮子商品中权重为![]()
④猪肉与其他禽肉在![]() 一篮子商品中权重约为
一篮子商品中权重约为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com