
分析 (1)当a=2时,求得f(x)的解析式和导数,可得切线的斜率和切点,由点斜式方程可得切线的方程;
(2)①求得f(x)的导数,可得f′(x)=lnx-ax=0有两个不同的实根,讨论当a≤0时,当a>0时,判断单调性可得极大值大于0,解不等式即可得到所求范围;
②由①知$0<{x_1}<\frac{1}{a}<{x_2}$,f(x1)是极小值,f(x2)是极大值,由f′(x1)=0,求得f(x1),运用二次函数的单调性,可得f(x1)<f(0)=0.
解答 解:(1)当a=2时,f(x)=xlnx-x2-x,f′(x)=lnx-2x,
可得f(1)=-2,f′(1)=-2,
曲线y=f(x)在(1,f(1))处的切线方程为y+2=-2(x-1),
即为y=-2x;
(2)①f′(x)=lnx-ax,函数y=f(x)有两个极值点x1、x2,
即f′(x)=lnx-ax=0有两个不同的实根,
当a≤0时,f′(x)单调递增,f′(x)=0不可能有两个不同的实根;
当a>0时,设h(x)=lnx-ax,h′(x)=$\frac{1-ax}{x}$,
若0<x<$\frac{1}{a}$时,h′(x)>0,h(x)单调递增,
若x>$\frac{1}{a}$时,h′(x)<0,h(x)单调递减,
可得h(x)的极大值h($\frac{1}{a}$)=-lna-1>0,解得0<a<$\frac{1}{e}$;
②证明:由①知$0<{x_1}<\frac{1}{a}<{x_2}$,f(x1)是极小值,f(x2)是极大值,
由f′(x)=lnx-ax=0,可得lnx1-ax1=0,
可得f(x1)=x1lnx1-$\frac{a}{2}$x12-x1=$\frac{a}{2}$x12-x1=$\frac{a}{2}$(x1-$\frac{1}{a}$)2-$\frac{1}{2a}$,
可得f(x1)在(0,$\frac{1}{a}$)单调递减,即有f(x1)<f(0)=0.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查分类讨论思想方法,以及函数方程的转化思想,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=10$\sqrt{3}$km,则OA2+OB2=200.
如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=10$\sqrt{3}$km,则OA2+OB2=200.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 152种 | B. | 54种 | C. | 90种 | D. | 126种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
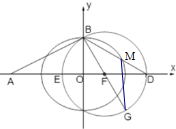 如图,已知F(c,0)是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点;圆F:(x-c)2+y2=a2与x轴交于D,E两点,其中E是椭圆C的左焦点.
如图,已知F(c,0)是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点;圆F:(x-c)2+y2=a2与x轴交于D,E两点,其中E是椭圆C的左焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com