
(本小题满分14分)已知圆C: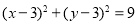 ,直线
,直线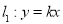 与圆C交于P、Q两个不同的点,M为P、Q的中点.
与圆C交于P、Q两个不同的点,M为P、Q的中点.

(Ⅰ)已知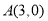 ,若
,若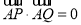 ,求实数
,求实数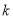 的值;
的值;
(Ⅱ)求点M的轨迹方程;
(Ⅲ)若直线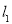 与
与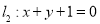 的交点为N,求证:
的交点为N,求证: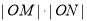 为定值.
为定值.
(1) ;
;
(2)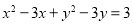
 ;
;
(3)定值为3;
【解析】
试题分析:(1)由向量的数量积为0,知两向量是垂直的,即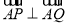 ,因为点A在圆C上故直线
,因为点A在圆C上故直线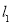 过圆心C
过圆心C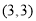 ,将点的坐标代入到直线方程中,得到
,将点的坐标代入到直线方程中,得到 ;(2)对于求轨迹方程的问题,一般来讲,求哪个点,就设设出哪个点的坐标,利用题意列出关系式,本题中,设
;(2)对于求轨迹方程的问题,一般来讲,求哪个点,就设设出哪个点的坐标,利用题意列出关系式,本题中,设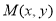 ,则
,则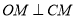 ,将坐标代入,化简可得出M的轨迹方程
,将坐标代入,化简可得出M的轨迹方程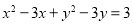
 ;(3)联立方程,通过韦达定理,得出M,N的坐标,从而求出
;(3)联立方程,通过韦达定理,得出M,N的坐标,从而求出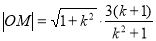 ,
,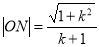 ,两者相乘,进行化简,得出定值是3.
,两者相乘,进行化简,得出定值是3.
试题解析:(Ⅰ)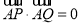 即
即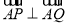 ,
,
因为点A在圆C上故直线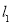 过圆心C
过圆心C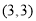 ,得
,得 3分
3分
(Ⅱ)设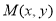 ,则
,则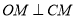 ,即
,即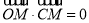 坐标代入得:
坐标代入得:
 化简得:
化简得: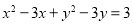
 8分
8分
(Ⅲ)设 将
将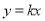 代入
代入 并整理得:
并整理得:
 则
则 为方程(*)的两根
为方程(*)的两根
∴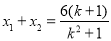

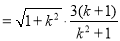 10分
10分
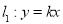 与
与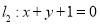 联立得交点
联立得交点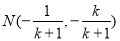
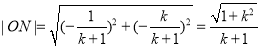 12分
12分
故:
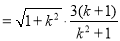
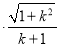 =3 (定值) 14分
=3 (定值) 14分
考点:?向量的数量积?圆的性质?韦达定理


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源:2014-2015学年江西省赣州市十二县高二上学期期中联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如下图表:
分组 | 频数 | 频率 |
[0,1) | 25 | y |
[1,2) | 0.19 | |
[2,3) | 50 | x |
[3,4) | 0.23 | |
[4,5) | 0.18 | |
[5,6] | 5 |

(Ⅰ)分别求出x,n,y的值;
(Ⅱ)若从样本中月均用水量在[5,6]内的5位居民a,b,c,d,e中任选2人作进一步的调查研究,求居民a被选中的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省赣州市十二县高二上学期期中联考理科数学试卷(解析版) 题型:选择题
若直线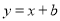 与曲线
与曲线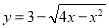 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( )
A.[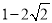 ,
,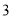 ] B.[
] B.[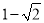 ,3]
,3]
C.[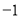 ,
,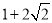 ] D.[
] D.[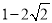 ,
,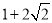 ]
]
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北长阳县第一高中高二上学期期中考试文科数学试卷(解析版) 题型:填空题
设 ABC的内角A,B,C的对边分别为
ABC的内角A,B,C的对边分别为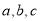 ,且
,且
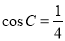 ,则
,则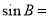 _________.
_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com