
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,过
,过![]() 上一点
上一点![]() 的切线与(2)所求轨迹
的切线与(2)所求轨迹![]() 交于点
交于点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)利用题中条件求出![]() 的值,然后根据离心率求出
的值,然后根据离心率求出![]() 的值,最后根据
的值,最后根据![]() 三者的关系求出
三者的关系求出![]() 的值,从而确定椭圆C的标准方程;
的值,从而确定椭圆C的标准方程;
(2)设![]() ,切点分别为
,切点分别为![]() ,
,![]() ,当
,当![]() 时,设切线方程为
时,设切线方程为![]() ,与椭圆联立消去
,与椭圆联立消去![]() ,得
,得![]() ,根据根的判别式
,根据根的判别式![]() ,化简得
,化简得![]() ,又因为
,又因为![]() 在椭圆
在椭圆![]() 外,
外, ![]() .又因为
.又因为![]() ,所以
,所以![]() ,即
,即![]() ,化简为
,化简为![]() ,
,
整理即可得![]() 的轨迹方程.
的轨迹方程.
(3)设![]() ,先求
,先求![]() .方法一:由相交弦定理,得
.方法一:由相交弦定理,得![]() .
.
方法二:切线![]() 的参数方程,将
的参数方程,将![]() 代入圆
代入圆![]() ,因为点
,因为点![]() 在圆
在圆![]() 内,整理可得
内,整理可得![]() .再利用公式求
.再利用公式求![]() ,所以
,所以![]() 证得.
证得.
(1)解:设![]() ,
,
由题设,得![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 的标准方程为
的标准方程为![]() .
.
(2)解:如图,设![]() ,切点分别为
,切点分别为![]() ,
,![]() ,
,
当![]() 时,设切线方程为
时,设切线方程为![]() ,
,
联立方程,得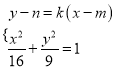 ,
,
消去![]() ,得
,得![]() ,①
,①
关于![]() 的方程①的判别式
的方程①的判别式![]() ,
,
化简,得![]() ,②
,②
关于![]() 的方程②的判别式
的方程②的判别式![]()
![]() ,
,
因为![]() 在椭圆
在椭圆![]() 外,
外,
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
关于![]() 的方程②有两个实根
的方程②有两个实根![]() ,
,![]() 分别是切线
分别是切线![]() ,
,![]() 的斜率,
的斜率,
因为![]() ,所以
,所以![]() ,即
,即![]() ,化简为
,化简为![]() ,
,
当![]() 时,可得
时,可得![]() ,满足
,满足![]() ,
,
所以![]() 的轨迹方程为
的轨迹方程为![]() .
.
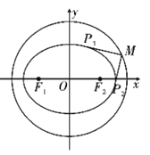
(3)证明:如图,设![]() ,先求
,先求![]() .
.
方法一:由相交弦定理,得
![]() .
.
方法二:切线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
![]() ,
,
代入圆![]() ,整理得
,整理得![]() ,
,
因为点![]() 在圆
在圆![]() 内,
内,
所以上述方程必有两个不等实根![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
所以![]()
![]() ,
,
当![]() 时,
时,![]() ,仍有
,仍有![]() .
.
再求![]() .
.
![]()
![]()
![]()
![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在正常数
,若存在正常数![]() 、
、![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,则称
均成立,则称![]() 是“控制增长函数”,在以下四个函数中:①
是“控制增长函数”,在以下四个函数中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增长函数”的有( )
.是“控制增长函数”的有( )
A.②③B.③④C.②③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 ,试估计该企业一个月(按30天计算)的经济损失的数学期望.
,试估计该企业一个月(按30天计算)的经济损失的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3个红球与3个黑球随机排成一行,从左到右依次在球上标记1,2,3,4,5,6,则红球上的数字之和小于黑球上的数字之和的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产旅游纪念品的工厂,拟在2017年度进行系列促销活动.经市场调查和测算,该纪念品的年销售量x(单位:万件)与年促销费用t(单位:万元)之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2017年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为“年平均每件生产成本的1.5倍”与“年平均每件所占促销费的一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
(1)请把该工厂2017年的年利润y(单位:万元)表示成促销费t(单位:万元)的函数;
(2)试问:当2017年的促销费投入多少万元时,该工厂的年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民的家庭收人情况,某社区组织工作人员从该社区的居民中随机抽取了![]() 户家庭进行问卷调查.经调查发现,这些家庭的月收人在
户家庭进行问卷调查.经调查发现,这些家庭的月收人在![]() 元到
元到![]() 元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一 、二、四小组的频率之比为
元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一 、二、四小组的频率之比为![]() ,且第四小组的频数为
,且第四小组的频数为![]() .
.
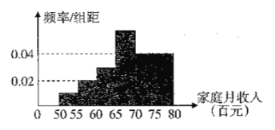
(1)求![]() ;
;
(2)求这![]() 户家庭月收人的众数与中位数(结果精确到
户家庭月收人的众数与中位数(结果精确到![]() );
);
(3)这![]() 户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取
户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取![]() 户家庭,并从这
户家庭,并从这![]() 户家庭中随机抽取
户家庭中随机抽取![]() 户家庭进行慰问,求这
户家庭进行慰问,求这![]() 户家庭月收入都不超过
户家庭月收入都不超过![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 过点
过点![]() ,
,![]() 为其焦点,过
为其焦点,过![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,动点
两点,动点![]() 满足
满足![]() 的垂心为原点
的垂心为原点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)求证:动点![]() 在定直线
在定直线![]() 上,并求
上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com