
分析 (1)由$\overrightarrow{α}$⊥($\overrightarrow{α}$-2$\overrightarrow{β}$)结合已知求得$\overrightarrow{α}•\overrightarrow{β}$,然后求出$|2\overrightarrow{α}+\overrightarrow{β}{|}^{2}$,则|2$\overrightarrow{α}$+$\overrightarrow{β}$|的值可求;
(2)由已知分别求出$(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})•\overrightarrow{a}$及$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|$,代入数量积求夹角公式求解.
解答 解:(1)|$\overrightarrow{α}$|=1,$\overrightarrow{β}$=(2,0),
由$\overrightarrow{α}$⊥($\overrightarrow{α}$-2$\overrightarrow{β}$),得$\overrightarrow{α}•(\overrightarrow{α}-2\overrightarrow{β})=|\overrightarrow{α}{|}^{2}-2\overrightarrow{α}•\overrightarrow{β}=0$,
∴$\overrightarrow{α}•\overrightarrow{β}=\frac{1}{2}$,
而$|2\overrightarrow{α}+\overrightarrow{β}{|}^{2}=4|\overrightarrow{α}{|}^{2}+4\overrightarrow{α}•\overrightarrow{β}+|\overrightarrow{β}{|}^{2}$=$4+4×\frac{1}{2}+4=10$,
∴|2$\overrightarrow{α}$+$\overrightarrow{β}$|=$\sqrt{10}$;
(2)$(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})•\overrightarrow{a}=|\overrightarrow{a}{|}^{2}+\overrightarrow{b}•\overrightarrow{a}+\overrightarrow{c}•\overrightarrow{a}$=$1+|\overrightarrow{b}||\overrightarrow{a}|cos120°+|\overrightarrow{c}||\overrightarrow{a}|cos120°$
=$1+2×1×(-\frac{1}{2})+3×1×(-\frac{1}{2})=-\frac{3}{2}$;
$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|=\sqrt{(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})^{2}}$=$\sqrt{|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}+|\overrightarrow{c}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}+2\overrightarrow{a}•\overrightarrow{c}+2\overrightarrow{b}•\overrightarrow{c}}$
$═\sqrt{1+4+9+2×1×2×(-\frac{1}{2})+2×1×3×(-\frac{1}{2})+2×2×3×(-\frac{1}{2})}$=$\sqrt{3}$.
设向量$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$与向量$\overrightarrow{a}$的夹角为θ,
∴cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})•\overrightarrow{a}}{|\overrightarrow{a}||\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|}$=$\frac{-\frac{3}{2}}{\sqrt{3}}=-\frac{\sqrt{3}}{2}$.
∵θ∈[0,π],
∴$θ=\frac{5π}{6}$.
即向量$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$与向量$\overrightarrow{a}$的夹角为$\frac{5π}{6}$.
点评 本题考查平面向量的数量积运算,考查了利用数量积求向量的夹角,考查运算能力,是中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
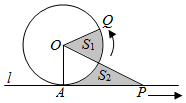 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )| A. | S1=S2 | B. | S1≤S2 | ||
| C. | S1≥S2 | D. | 先S1<S2,再S1=S2,最后S1>S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | 1$+\frac{1}{2}$$+\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ | D. | 非以上答案 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-a)∪(5a,+∞) | B. | (-∞,5a)∪(-a,+∞) | C. | (5a,-a) | D. | (a,-5a) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | b>a>c | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ≥2 | B. | λ>3 | C. | λ≥3 | D. | λ>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com