解答:
解:(b,c)的所有可能的取值有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种.…(3分)
(1)要使方程x
2+bx+c=0有实根,必须满足△=b
2-4c≥0,符合条件的有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(4,4),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共19种.
∴方程x
2+bx+c=0有实根的概率为
P=. …(6分)
(2)由(1)得在先后两次出现的点数中有5的条件下,方程x
2+bx+c=0有实根结果有:
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,5),共7种.
∴在先后两次出现的点数中有5的条件下,方程x
2+bx+c=0有实根的概率为
P=.…(9分)
(3)试验的全部可能的结果所构成的区域为{(b,c)|1≤b≤4,2≤c≤4}.
由f(-2)>0得,4-2b+c>0,
则构成事件{f(-2)>0成立}的区域为{(b,c)|1≤b≤4,2≤c≤4,4-2b+c>0}.
在b-O-c系中画出此不等式表示的平面区域,图中的阴影部分区域为事件构成的区域,

又b∈[1,4],c∈[2,4],它表示的平面区域是一个矩形,根据几何概型可得,
所以所求事件{f(-2)>0成立}的概率为p=
=. …(12分)
点评:本题考查了几何概型、古典概率下的事件概率公式,关键是根据题意判断出概率符合的模型.古典概率类型题的求解,首先列出所有的实验结果每种结果,代入古典概率的计算公式:P(A)=
(其中n是试验的所有结果,m是基本事件的结果数);几何概型下的概率应用图解法来表示出所有的满足条件的区域,代入公式求解.




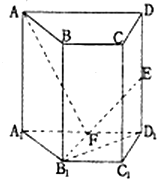 如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.

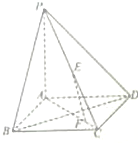 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.