
分析 由题意知,在棱锥P-ABC中,△PAC,△PBC都是等腰直角三角形,取PC的中点D,则PC垂直于面ABD,棱锥P-ABC的体积为两个棱锥P-ABD和C-ABD的体积和,由此能求出棱锥P-ABC的体积.
解答 解:如图所示,由题意知,在棱锥P-ABC中,△PAC,△PBC都是等腰直角三角形,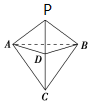
其中AB=2,PC=4,PA=AC=PB=BC=2$\sqrt{2}$.
取PC的中点D,则PC垂直于面ABD,D是球心,DA=DB=2,
∴棱锥P-ABC的体积为两个棱锥P-ABD和C-ABD的体积和,
S△ABD=$\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$,
∴棱锥P-ABC的体积V=$\frac{1}{3}$•PC•S△ADB=$\frac{1}{3}$×4×$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|-1≤x≤2} | C. | {x|0≤x≤2} | D. | {x|-1≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:5 | B. | 9:25 | C. | 5:$\sqrt{41}$ | D. | 7:9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2 | B. | 2:5 | C. | 1:3 | D. | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
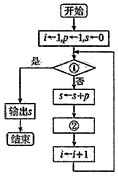 给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),
给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
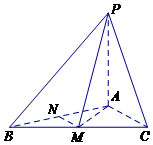 在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.
在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com