
分析 (Ⅰ)利用抛物线定义“到定点距离等于到定直线距离的点的轨迹”求动点P的轨迹;
(Ⅱ)直线y=k(x-1)与抛物线方程联立,可得y2-$\frac{4}{k}$y-4=0,利用韦达定理及抛物线的定义,即可求出$\frac{1}{|MF|}$+$\frac{1}{|NF|}$为定值.
解答 (Ⅰ)解:因为动点P到直线x=-2的距离比它到点F(1,0)的距离大1,
所以动点P到直线x=-1的距离与它到点F(1,0)的距离相等,
故所求轨迹为:以原点为顶点,开口向右的抛物线y2=4x.
(Ⅱ)证明:直线y=k(x-1)与抛物线方程联立,可得y2-$\frac{4}{k}$y-4=0,
设M(x1,y1),N(x2,y2),y1+y2=$\frac{4}{k}$,y1y2=-4,
∴$\frac{1}{|MF|}$+$\frac{1}{|NF|}$=$\frac{1}{{x}_{1}+1}$+$\frac{1}{{x}_{2}+1}$=$\frac{{x}_{1}+{x}_{2}+2}{{x}_{1}{x}_{2}+{x}_{1}+{x}_{2}+1}$=$\frac{{x}_{1}+{x}_{2}+2}{\frac{{{y}_{1}}^{2}}{4}•\frac{{{y}_{2}}^{2}}{4}+{x}_{1}+{x}_{2}+1}$=$\frac{{x}_{1}+{x}_{2}+2}{{x}_{1}+{x}_{2}+2}$=1,
∴$\frac{1}{|MF|}$+$\frac{1}{|NF|}$为定值.
点评 本题考查抛物线定义,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
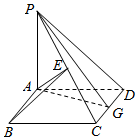 如图,ABCD是边长为a的正方形,PA⊥平面ABCD.
如图,ABCD是边长为a的正方形,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1:2 | B. | 1:$\sqrt{2}$:1 | C. | 1:1:1 | D. | 1:1:$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | 若α⊥β,α∩β=n,m⊥n,则m⊥α | D. | 若α∩β=n,m∥α,m∥β,则m∥n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com