Question

14．向量$\overrightarrow{m}$和$\overrightarrow{n}$的起点都在坐标原点．$\overrightarrow{m}$=（$\frac{{t}^{2}-5}{2a}$，t）．$\overrightarrow{n}$=（-$\frac{{t}^{2-5}}{2b}$，t）（a，b为正常数，t∈R）．
（1）当实数t变化时．求$\overrightarrow{m}$和$\overrightarrow{n}$的终点的运动轨迹C₁和C₂
（2）有长方形ABCD的四个顶点都在（1）中的C₁与C₂所围成图形的边界上．且长方形各边分别与x轴．y轴平行．顶点A，B在C₂上．A（x，y），求该长方形的面积f（x）及其定义域；
（3）在上述条件下．若所有长方形ABCD中面积最大的是正方形，求a与b的关系．

Answer 1

分析 （1）设$\overrightarrow{m}$=（x，y），则（x，y）=（$\frac{{t}^{2}-5}{2a}$，t），设$\overrightarrow{n}$=（x，y），则（x，y）=（-$\frac{{t}^{2}-5}{2b}$，t），由此能求出$\overrightarrow{m}$，$\overrightarrow{n}$的终点的轨迹．
（2）设A在第一象限，由题意A（x，$\sqrt{-2bx+5}$），B（x，-$\sqrt{-2bx+5}$），设D（x₀，$\sqrt{-2bx+5}$），由此能求出该长方形的面积f（x）及其定义域．
（3）设g（x）=x²（-2bx+5），（0$≤x≤\frac{5}{2b}$），则f（x）与g（x）同步最大，故只需研究使g（x）最大时x的取值，由此利用导数性质能求出结果．

解答 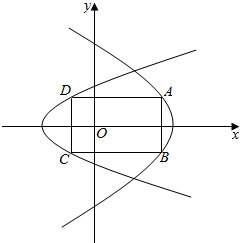解：（1）设$\overrightarrow{m}$=（x，y），则（x，y）=（$\frac{{t}^{2}-5}{2a}$，t），
∴$\left\{\begin{array}{l}{x=\frac{{t}^{2}-5}{2a}}\\{y=t}\end{array}\right.$，∴y²=-2bx+5，
设$\overrightarrow{n}$=（x，y），则（x，y）=（-$\frac{{t}^{2}-5}{2b}$，t），
∴$\left\{\begin{array}{l}{x=-\frac{{t}^{2}-5}{2b}}\\{y=t}\end{array}\right.$，∴y²=-2bx+5，
∴$\overrightarrow{m}$，$\overrightarrow{n}$的终点的轨迹分别是抛物线C₁：y²=2ax+5和C₂：y²=-2bx+5．
（2）设A在第一象限，由点A在C₁上得y=$\sqrt{-2bx+5}$，
∴A（x，$\sqrt{-2bx+5}$），B（x，-$\sqrt{-2bx+5}$），
∵AD∥x轴，故设D（x₀，$\sqrt{-2bx+5}$），
代入C₁：y²=2ax+5，得-2bx+5=2ax+5，∴${x}_{0}=-\frac{b}{a}x$，
∴D（-$\frac{b}{a}x$，$\sqrt{-2bx+5}$），∴|AB|=2$\sqrt{-2bx+5}$，
∴|AD|=x-（-$\frac{b}{a}x$）=$\frac{a+b}{a}$x．
∴f（x）=|AB|•|CD|=$\frac{2（a+b）}{a}•x\sqrt{-2bx+5}$，
由$\left\{\begin{array}{l}{x≥0}\\{-2bx+5≥0}\end{array}\right.$，得0≤x≤$\frac{5}{2b}$．
（3）设g（x）=x²（-2bx+5），（0$≤x≤\frac{5}{2b}$），
则f（x）与g（x）同步最大，故只需研究使g（x）最大时x的取值，
令g′（x）=2x（-2bx+5）+x²（-2b）=-2x（3bx-5）=0，
则${x}_{1}=0，{x}_{2}=\frac{5}{3b}$，则增减表如下：

x	0	（0，$\frac{5}{3b}$）	$\frac{5}{3b}$	（$\frac{5}{3b}$，$\frac{5}{2b}$）	$\frac{5}{2b}$
g′（x）		+	0	-
g（x）	0	↑	极大值	↓	0

当x=$\frac{5}{3b}$时，g（x）取最大值g（$\frac{5}{3b}$）=$\frac{25}{9{b}^{2}}•\frac{5}{3}$=$\frac{125}{27{b}^{2}}$＞0，
∴$x=\frac{5}{3b}$时，g（x）取最大值，此时f（x）取最大值，且ABCD为正方形，
而|AB|=2$\sqrt{-2b•\frac{5}{3}+5}$=$\frac{2}{3}\sqrt{15}$，|AD|=$\frac{5}{3b}$（1+$\frac{b}{a}$）=$\frac{5}{3}$（$\frac{1}{a}+\frac{1}{b}$），
由|AB|=|AD|，得：$\frac{2}{3}\sqrt{15}$=$\frac{5}{3}$（$\frac{1}{a}+\frac{1}{b}$），
∴$\frac{1}{a}+\frac{1}{b}$=$\frac{2}{5}\sqrt{15}$，
∴a，b应确定的条件是$\frac{1}{a}+\frac{1}{b}=\frac{2\sqrt{15}}{5}$，a＞0，b＞0．

点评 高考题主要考查知识的交汇点，本题体现了这一高考发展趋势，主要考查向量、轨迹、坐标法，函数最大值等知识点，综合性强，难度大．