
分析 (1)由a1=2,${a_{n+1}}=\frac{{2{a_n}-9}}{{{a_n}-4}}({n∈{N^+}})$,分别令n=1,2,3,即可得出;
(2)由(1)猜想:an=3-$\frac{1}{n}$,利用数学归纳法证明即可,
(3)先求出bn=$\frac{1}{n}$-$\frac{1}{n+1}$,裂项求和即可.
解答 解:(1){an}满足${a_{n+1}}=\frac{{2{a_n}-9}}{{{a_n}-4}}({n∈{N^+}})$,且a1=2,
∴a2=$\frac{2{a}_{1}-9}{{a}_{2}-4}$=$\frac{2×2-9}{2-4}$=$\frac{5}{2}$,a3=$\frac{2×\frac{5}{2}-9}{\frac{5}{2}-4}$=$\frac{8}{3}$,a3=$\frac{2×\frac{8}{3}-9}{\frac{8}{3}-4}$=$\frac{11}{4}$,
(2)可以猜想an=3-$\frac{1}{n}$,
证明如下:①当n=1时,猜想当然显然成立;
②假设当n=k(k∈N+)时猜想成立,
即ak=3-$\frac{1}{k}$,则ak+1=$\frac{2{a}_{k}-9}{{a}_{k}-4}$=$\frac{-3-\frac{2}{k}}{-1-\frac{1}{k}}$=$\frac{3k+2}{k+1}$=3-$\frac{1}{k+1}$,
故当然n=k+1时猜想成立,
由①②可知,猜想成立;
(3)由(2)知bn=$\frac{1}{n+1}•\frac{1}{n}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故Tn=$\sum_{i=1}^{n}$($\frac{1}{i}$-$\frac{1}{i+1}$)=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查了数学归纳法、递推公式、数列的通项公式,考查了猜想归纳能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
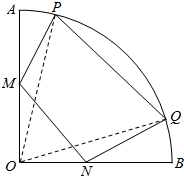 如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.
如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2f(-15)<f(-6),e2f(-11)<f(-20) | B. | e2f(-15)>f(-6),e2f(-11)>f(-20) | ||
| C. | e2f(-15)<f(-6),e2f(-11)>f(-20) | D. | e2f(-15)>f(-6),e2f(-11)<f(-20) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1:2 | B. | 1:$\sqrt{2}$:1 | C. | 1:1:1 | D. | 1:1:$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com