
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | -$\frac{1}{2}$±$\frac{\sqrt{3}}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 圆O的半径为1,P为圆周上一点,现将如图放置的边长为1的正三角形(实线所示,正三角形的顶点A和点P重合)沿着圆周顺时针滚动,经过若干次滚动,点A第一次回到点P的位置,则点A走过的路径的长度为( )
圆O的半径为1,P为圆周上一点,现将如图放置的边长为1的正三角形(实线所示,正三角形的顶点A和点P重合)沿着圆周顺时针滚动,经过若干次滚动,点A第一次回到点P的位置,则点A走过的路径的长度为( )| A. | π | B. | $\frac{4}{3}$π | C. | $\frac{5}{3}$π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
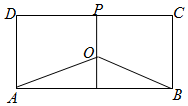 节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.
节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com