
 圆O的半径为1,P为圆周上一点,现将如图放置的边长为1的正三角形(实线所示,正三角形的顶点A和点P重合)沿着圆周顺时针滚动,经过若干次滚动,点A第一次回到点P的位置,则点A走过的路径的长度为( )
圆O的半径为1,P为圆周上一点,现将如图放置的边长为1的正三角形(实线所示,正三角形的顶点A和点P重合)沿着圆周顺时针滚动,经过若干次滚动,点A第一次回到点P的位置,则点A走过的路径的长度为( )| A. | π | B. | $\frac{4}{3}$π | C. | $\frac{5}{3}$π | D. | 2π |
分析 由图可知:圆O的半径r=1,正三角形的边长a=1,以正三角形的边为弦时所对的圆心角为$\frac{π}{3}$,当点A首次回到点P的位置时,正三角形滚动了6次,分别算出转3次的长度,即可得出.
解答 解:由图可知:∵圆O的半径r=1,正三角形的边长a=1,
∴以正三角形的边为弦时所对的圆心角为$\frac{π}{3}$,
∴当点A首次回到点P的位置时,正方形滚动了共6次,
设第i次滚动,点A的路程为Ai,
则A1=$\frac{π}{3}$×|AB|=$\frac{π}{3}$,
A2=$\frac{π}{3}$×|AO|=$\frac{π}{3}$,
A3=0,
∴点A所走过的路径的长度为2(A1+A2+A3)=$\frac{4π}{3}$.
故选:B.
点评 本题考查了正方形与圆的性质、旋转的性质、弧长的计算公式,考查了数形结合、分类讨论的思想方法,考查了分析问题与解决问题的能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
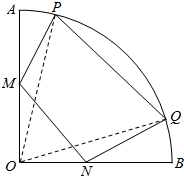 如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.
如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com