
| A. | e2f(-15)<f(-6),e2f(-11)<f(-20) | B. | e2f(-15)>f(-6),e2f(-11)>f(-20) | ||
| C. | e2f(-15)<f(-6),e2f(-11)>f(-20) | D. | e2f(-15)>f(-6),e2f(-11)<f(-20) |
分析 根据函数奇偶性和对称性求出函数f(x)是周期为8的周期函数,构造函数h(x)=$\frac{f(x)}{{e}^{2x}}$,判断函数的单调性进行比较即可.
解答 解:设h(x)=$\frac{f(x)}{{e}^{2x}}$,则h′(x)=$\frac{f′(x){e}^{2x}-f(x){e}^{2x}•2}{({e}^{x})^{2}}$=$\frac{f′(x)-2f(x)}{{e}^{x}}$.
∵当x∈[0,4]时,f(x)可导且满足f′(x)>2f(x),
∴此时h′(x)>0,即函数h(x)此时单调递增.
∵定义域为R的偶函数f(x)的图象关于直线x=4对称,
∴f(4+x)=f(4-x)=f(x-4),
即f(x+8)=f(x),即函数f(x)是周期为8的周期函数,
则f(-15)=f(-16+1)=f(1),f(-6)=f(2),
f(-11)=f(-8-3)=f(-3)=f(3),f(-20)=f(-16-4)=f(-4)=f(4),
由h(2)>h(1),即$\frac{f(2)}{{e}^{4}}>\frac{f(1)}{{e}^{2}}$,则f(2)>e2f(1),即f(-6)>e2f(-15),
由h(4)>h(3),即$\frac{f(4)}{{e}^{8}}$>$\frac{f(3)}{{e}^{6}}$,则f(4)>e2f(3),即f(-20)>e2f(-11),
故选:A.
点评 本题主要考查函数值的大小比较,根据函数奇偶性和对称性的性质判断函数的周期性,利用构造法构造函数,利用导数研究函数的单调性是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | -$\frac{1}{2}$±$\frac{\sqrt{3}}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
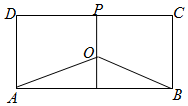 节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.
节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c至少与a、b中的一条相交 | B. | c至多与a、b中的一条相交 | ||
| C. | c与a、b都相交 | D. | c与a、b都不相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com