
分析 求出双曲线的渐近线方程,讨论直线与渐近线平行和直线与双曲线相切的条件,解方程即可得到所求值.
解答 解:双曲线2x2-y2=2的渐近线方程为y=±$\sqrt{2}$x,
当直线y=kx-1与渐近线平行时,即k=±$\sqrt{2}$时,
与双曲线有且仅有一个公共点;
当直线y=kx-1与双曲线相切,与双曲线有且仅有一个公共点.
代入双曲线的方程,可得(2-k2)x2+2kx-3=0,
由判别式4k2+12(2-k2)=0,
解得k=±$\sqrt{3}$,
综上可得,k=±$\sqrt{2}$或±$\sqrt{3}$.
故答案为:±$\sqrt{2}$或±$\sqrt{3}$.
点评 本题考查直线和双曲线的位置关系,注意联立直线方程和双曲线的方程,运用判别式为0,同时注意双曲线的渐近线平行的直线,属于中档题和易错题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | e2f(-15)<f(-6),e2f(-11)<f(-20) | B. | e2f(-15)>f(-6),e2f(-11)>f(-20) | ||
| C. | e2f(-15)<f(-6),e2f(-11)>f(-20) | D. | e2f(-15)>f(-6),e2f(-11)<f(-20) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
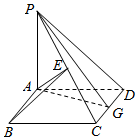 如图,ABCD是边长为a的正方形,PA⊥平面ABCD.
如图,ABCD是边长为a的正方形,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意三点确定一个平面 | |
| B. | 任意四点确定一个平面 | |
| C. | 三条平行直线最多确定一个平面 | |
| D. | 正方体ABCD-A1B1C1D1中,AB与CC1异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1:2 | B. | 1:$\sqrt{2}$:1 | C. | 1:1:1 | D. | 1:1:$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≤-$\frac{4}{3}$或k≥-$\frac{3}{4}$ | B. | k≤$\frac{3}{4}$或k≥$\frac{4}{3}$ | C. | -$\frac{4}{3}$≤k≤-$\frac{3}{4}$ | D. | $\frac{3}{4}$≤k≤$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
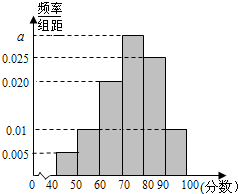 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com