在△ABC中.角A.B.C所对的边分别为a.b.c.且a=5.b=8.C=60°.则$\overrightarrow{BC}$•$\overrightarrow{CA}$的值为-20．题目和参考答案——青夏教育精英家教网—

3．在△ABC中，角A、B、C所对的边分别为a、b、c，且a=5，b=8，C=60°，则$\overrightarrow{BC}$•$\overrightarrow{CA}$的值为-20．

分析根据条件可知，$|\overrightarrow{BC}|=5$，$|\overrightarrow{CA}|=8$，$\overrightarrow{BC}$与$\overrightarrow{CA}$的夹角为120°，这样进行向量数量积的计算便可得出$\overrightarrow{BC}•\overrightarrow{CA}$的值．

解答解：如图，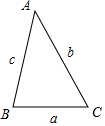

$\overrightarrow{BC}•\overrightarrow{CA}=|\overrightarrow{BC}||\overrightarrow{CA}|cos120°$=$5×8×（-\frac{1}{2}）=-20$．
故答案为：-20．

点评考查向量夹角的概念，以及向量数量积的计算公式．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

1．根据图象特征分析以下函数：
①f（x）=3-x ②f（x）=x²-3x ③f（x）=-$\frac{1}{x}$ ④f（x）=-|x|⑤y=ln（x+1）
其中在（0，+∞）上是增函数的是③⑤；（只填序号即可）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．已知点M（3，0），两直线l₁：2x-y-2=0与l₂：x+y+3=0．
（1）过点M的直线l与l₁，l₂相交于P，Q两点，且线段PQ恰好被M所平分，求直线l的方程；
（2）求l₁关于l₂对称的直线l₃的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．设函数f（x）定义在（0，+∞）上的单调函数，且满足条件f（4）=1，对任意x₁，x₂∈（0，+∞），有f（x₁•x₂）=f（x₁）+f（x₂）．
（1）求f（1）的值；
（2）如果f（x+6）＞2，求x的取值范围；
（3）若对于任意x∈[1，4]都有f（x）≥m²+m-1恒成立，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．