
【题目】已知函数f(x)=![]()
(1)求f(x)>0的解集;
(2)若x∈R时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)(0,+∞)(2)[![]() ,+∞)
,+∞)
【解析】
(1)通过对f(x)求导,可得x∈R时,f′(x)≥0,所以f(x)在(﹣∞,+∞)上单调递增,又f(0)=0,x∈(0,+∞)时f(x)>0,不等式得解;
(2)若x∈R时,![]() 恒成立,不等式转化为2e
恒成立,不等式转化为2e![]() ex
ex![]() (x∈R),因为都是偶函数,所以只需x∈[0,+∞)时,2e
(x∈R),因为都是偶函数,所以只需x∈[0,+∞)时,2e![]() e2x﹣1≥0成立即可,构造新的函数F(x)=2e
e2x﹣1≥0成立即可,构造新的函数F(x)=2e![]() e2x﹣1,求导后再对导函数进行分类讨论,可得实数m的取值范围.
e2x﹣1,求导后再对导函数进行分类讨论,可得实数m的取值范围.
(1)因为f(x)=![]() ,则f′(x)=
,则f′(x)=![]() ;
;
所以x∈R时,f′(x)≥0,
所以f(x)在(﹣∞,+∞)上单调递增,又f(0)=0,
所以x∈(﹣∞,0)时,f(x)<0,
x∈(0,+∞)时f(x)>0,
∴f(x)>0的解集为(0,+∞).
(2)因为x∈R时,2e![]() e2x+1恒成立,
e2x+1恒成立,
等价于![]() 恒成立,
恒成立,
即2e![]() ex
ex![]() (x∈R),
(x∈R),
因为都是偶函数,
所以只需x∈[0,+∞)时,2e![]() e2x﹣1≥0成立即可,
e2x﹣1≥0成立即可,
令F(x)=2e![]() e2x﹣1,F(0)=0,
e2x﹣1,F(0)=0,
F′(x)=2(2mx+1)e![]() 2e2x=2e2x[(2mx+1)e
2e2x=2e2x[(2mx+1)e![]() 1],F′(0)=0,
1],F′(0)=0,
令G(x)=(2mx+1)e![]() 1,G(0)=0,
1,G(0)=0,
G′(x)=2me![]() (2mx+1)(2mx﹣1)e
(2mx+1)(2mx﹣1)e![]() (4m2x2+2m﹣1)e
(4m2x2+2m﹣1)e![]()
①当2m﹣1≥0,即m![]() 时,G′(x)≥0,所以G(x)在[0,+∞)上单调递增,
时,G′(x)≥0,所以G(x)在[0,+∞)上单调递增,
又因为G(0)=0,所以x∈[0,+∞)时,G(x)≥0,即F′(x)≥0,
所以F(x)在[0,+∞)上单调递增,又因为F(0)=0,所以x∈[0,+∞)时,F(x)≥0,所以m![]() 时满足要求;
时满足要求;
②当m=0,x=1时,2e<e2+1,不成立,所以m≠0;
③当2m﹣1<0且m≠0时,即m![]() 且m≠0时,x∈
且m≠0时,x∈ 上单调递减,
上单调递减,
又因为G(0)=0,所以x∈ 时,G(x)<0,即F′(x)<0,
时,G(x)<0,即F′(x)<0,
所以F(x)在 上单调递减,
上单调递减,
又因为F(0)=0,所以x∈ 时,F(x)<0,
时,F(x)<0,
所以m![]() 且m≠0时不满足要求.
且m≠0时不满足要求.
综上所述,实数m的取值范围是[![]() ,+∞).
,+∞).


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】
给定椭圆![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为![]() ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为![]() .
.
(I)求椭圆C的方程和其“准圆”方程;
(II )点P是椭圆C的“准圆”上的一个动点,过点P作直线![]() ,使得
,使得![]() 与椭圆C都只有一个交点,且
与椭圆C都只有一个交点,且![]() 分别交其“准圆”于点M,N.
分别交其“准圆”于点M,N.
(1)当P为“准圆”与![]() 轴正半轴的交点时,求
轴正半轴的交点时,求![]() 的方程;
的方程;
(2)求证:|MN|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,O为线段AC上一点,平面ADC⊥平面ABC,且△ADO,△ABO为等腰直角三角形,斜边AO=4![]() .
.
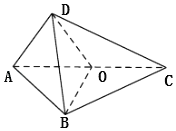
(Ⅰ)求证:AC⊥BD;
(Ⅱ)将△BDO绕DO旋转一周,求所得旋转体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() ,
,![]() 轴被曲线
轴被曲线![]() 截得的线段长等于C1的长半轴长.
截得的线段长等于C1的长半轴长.
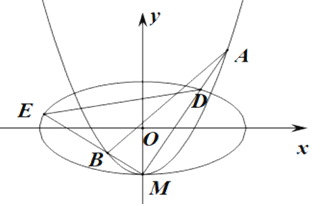
(1)求实数b的值;
(2)设C2与![]() 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线![]() 与C2相交于点A、B,直线MA、MB分别与C1交于点D、E.
与C2相交于点A、B,直线MA、MB分别与C1交于点D、E.
①证明:![]() ;
;
②记△MAB,△MDE的面积分别是![]() 若
若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于双曲线![]() :
:![]() (
(![]() ),若点
),若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的外部;若点
的外部;若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的内部.
的内部.
(1)证明:直线![]() 上的点都在
上的点都在![]() 的外部.
的外部.
(2)若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 的内部或
的内部或![]() 上,求
上,求![]() 的最小值.
的最小值.
(3)若![]() 过点
过点![]() ,圆
,圆![]() (
(![]() )在
)在![]() 内部及
内部及![]() 上的点构成的圆弧长等于该圆周长的一半,求
上的点构成的圆弧长等于该圆周长的一半,求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com