
【题目】已知圆![]() 、圆
、圆![]() 均满足圆心在直线
均满足圆心在直线![]() :
: ![]() 上,过点
上,过点![]() ,且与直线l2:x=-1相切.
,且与直线l2:x=-1相切.
(1)当![]() 时,求圆
时,求圆![]() ,圆
,圆![]() 的标准方程;
的标准方程;
(2)直线l2与圆![]() 、圆
、圆![]() 分别相切于A,B两点,求
分别相切于A,B两点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)设出圆的标准方程,圆心为(an,bn),半径为rm,根据已知条件列方程,解方程即可;
(2)根据圆过(1,0),与x=-1相切,且圆心在直线x-my-2=0上,得方程b2-4mb-8=0,结合图象,用含m的式子表示出![]() ,进而求出
,进而求出![]() 的最小值。
的最小值。
设圆![]() .
.
依题意得: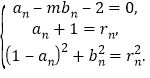
消去![]() 得
得
消去![]() 得
得![]() .
.
(1)当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以圆![]() ,圆
,圆![]() 的标准方程分别为:
的标准方程分别为:![]() ,
,![]() .
.
(2)根据题意,如图:
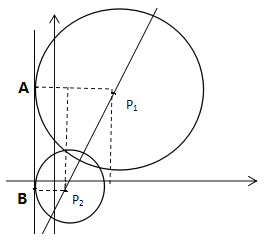
设圆的方程为(x-a)2+(y-b)2=r2,
已知过(1,0),得方程(1-a)2+b2=r2 ① ![]()
已知圆心在直线![]()
![]() 上 ,得方程a-mb-2=0,得a=mb+2 ②,
上 ,得方程a-mb-2=0,得a=mb+2 ②,
已知直线l :x=-1与圆切与A,B,得r=a+1 ③
综合①②③得b2-4mb-8=0,
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.
故当且仅当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆经过点
为圆心的圆经过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 和
和![]() ,且
,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)求圆![]() 的方程;
的方程;
(3)设点![]() 在圆
在圆![]() 上,试问使△
上,试问使△![]() 的面积等于8的点
的面积等于8的点![]() 共有几个?证明你的结论.
共有几个?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知 ![]() cosB+
cosB+ ![]() cosA=
cosA= ![]() (I)求∠C的大小;
(I)求∠C的大小;
(II)求sinB﹣ ![]() sinA的最小值.
sinA的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足 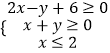 ,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
A.[﹣1,2]
B.[﹣2,1]
C.[2,3]
D.[﹣1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 中点.
中点.
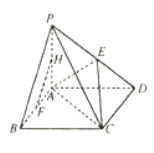
(1)证明: ![]() 平面
平面![]() ;
;
(2)若平面![]() 底面
底面![]() ,
, ![]() ,试在
,试在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() ,并证明此结论.
,并证明此结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x+ ![]() .
.
(Ⅰ)若a=﹣2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若关于x的不等式f(x)≥a+1在(0,+∞)上恒成立,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0. 05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com