
| A、39 |
| B、38 |
| C、39-1 |
| D、38-1 |
| C | 4 n |


科目:高中数学 来源: 题型:
 黑白两种颜色的正方形地砖依照如图的规律拼成若干个图形,现将一粒豆子随机撒在第10个图中,则豆子落在白色地砖上的概率是( )
黑白两种颜色的正方形地砖依照如图的规律拼成若干个图形,现将一粒豆子随机撒在第10个图中,则豆子落在白色地砖上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||
B、(
| ||
C、(
| ||
D、(0,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
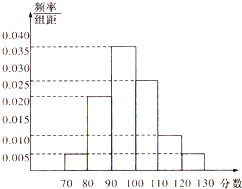 我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.
我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com