
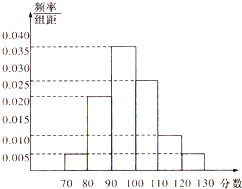
 ��У��1201��1202��1203��1204�ĸ��࣬���������ȡ����ѧ�����гɼ�ͳ�ƣ����౻��ȡѧ��������ǡ�óɵȲ����У��������ٵİ౻��ȡ��24�ˣ���ȡ��ѧ���IJ��Գɼ�ͳ�ƽ����������ͼ��ʾƵ�ʷֲ�ֱ��ͼ�����з�����[120��130]������Ϊ6�ˣ�
��У��1201��1202��1203��1204�ĸ��࣬���������ȡ����ѧ�����гɼ�ͳ�ƣ����౻��ȡѧ��������ǡ�óɵȲ����У��������ٵİ౻��ȡ��24�ˣ���ȡ��ѧ���IJ��Գɼ�ͳ�ƽ����������ͼ��ʾƵ�ʷֲ�ֱ��ͼ�����з�����[120��130]������Ϊ6�ˣ�| 6 |
| 0.05 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��39 |
| B��38 |
| C��39-1 |
| D��38-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
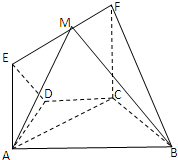 ��ͼ���ڼ�����ABCDEF�У�AB��CD��AD=DC=CB=1����ABC=60�㣬�ı���ACFEΪ���Σ�ƽ��ACFE��ƽ��ABCD��CF=1��
��ͼ���ڼ�����ABCDEF�У�AB��CD��AD=DC=CB=1����ABC=60�㣬�ı���ACFEΪ���Σ�ƽ��ACFE��ƽ��ABCD��CF=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| n(n+1) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| z+i |
| z-1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com