Question

14．已知实数x，y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x＜2}\\{x+y-1≥0}\end{array}\right.$，则z=2x-2y-3的取值范围是（　　）

• A． [-$\frac{1}{3}$，3]
• B． [-2，3]
• C． [-$\frac{1}{3}$，3）
• D． $[-\frac{11}{3}，3）$

Answer 1

分析 根据画出不等式组表示的平面区域，利用数形结合结合目标函数的意义，利用平移即可得到结论．

解答 解：不等式对应的平面区域如图：（阴影部分）．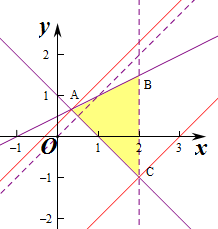 
由z=2x-2y-3得y=x-$\frac{3+z}{2}$，平移直线y=x-$\frac{3+z}{2}$，
由平移可知当直线y=x-$\frac{3+z}{2}$，经过点C时，
直线y=x-$\frac{3+z}{2}$的截距最小，此时z取得最大值，
由$\left\{\begin{array}{l}{x=2}\\{x+y-1=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$，即C（2，-1），
此时z=2x-2y-3=4+2-3=3，
可知当直线y=x-$\frac{3+z}{2}$，经过点A时，
直线y=y=x-$\frac{3+z}{2}$的截距最大，此时z取得最小值，
由$\left\{\begin{array}{l}{x-2y+1=0}\\{x+y-1=0}\end{array}\right.$，得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$，即A（$\frac{1}{3}$，$\frac{2}{3}$）
代入z=2x-2y-3得z=2×$\frac{1}{3}$-2×$\frac{2}{3}$-3=-$\frac{11}{3}$，
故z∈[-$\frac{11}{3}$，3）
故选：D．

点评 本题主要考查线性规划的应用，利用数形结合是解决线性规划问题中的基本方法．