
分析 (Ⅰ)由离心率及椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切求出a,b,从而得到椭圆的方程;
(Ⅱ)设出直线方程,与椭圆方程联立,求出|AB|的距离,表示出△OAB的面积,利用基本不等式求最值.
解答 解:(Ⅰ)由题意,e2=($\frac{c}{a}$)2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
则a2=2b2;
又∵原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切,
则b=$\frac{|\sqrt{2}|}{\sqrt{1+1}}$=1,
∴b2=1,a2=2;
∴椭圆C的方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)证明:设直线l的方程为y=kx+m,k=1或2,A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$可得(1+2k2)x2+4kmx+2m2-2=0,
所以△=16k2-8m2+8>0(*)
x1+x2=$\frac{-4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{(-\frac{4km}{1+2{k}^{2}})^{2}-4•\frac{2{m}^{2}-2}{1+2{k}^{2}}}$
=$\frac{\sqrt{1+{k}^{2}}}{1+2{k}^{2}}$•$\sqrt{8(2{k}^{2}-{m}^{2}+1)}$,
由原点O到直线y=kx+m的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,
S△AOB=$\frac{1}{2}$|AB|•d=$\frac{\sqrt{2}}{1+2{k}^{2}}$$\sqrt{{m}^{2}(2{k}^{2}-{m}^{2}+1)}$,
当k=1时,由S△AOB=$\frac{\sqrt{2}}{3}$$\sqrt{{m}^{2}(3-{m}^{2})}$,
当m2=$\frac{3}{2}$时,S△AOB的面积的最大值为S1=$\frac{\sqrt{2}}{2}$,验证(*)成立;
当k=2时,由S△AOB=$\frac{\sqrt{2}}{9}$$\sqrt{{m}^{2}(9-{m}^{2})}$,
当m2=$\frac{9}{2}$时,S△AOB的面积的最大值为S2=$\frac{\sqrt{2}}{2}$,验证(*)成立.
即有S1=S2.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率公式和方程的运用,联立直线方程,运用韦达定理和弦长公式,以及基本不等式求最值,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 分组 (日销售量) | 频率 (甲种酸奶) |
| [0,10] | 0.10 |
| (10,20] | 0.20 |
| (20,30] | 0.30 |
| (30,40] | 0.25 |
| (40,50] | 0.15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y-1)2=1 | B. | x2+(y+1)2=1 | C. | (x-1)2+y2=1 | D. | (x+1)2+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
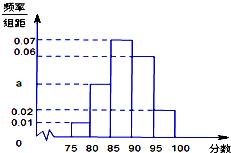 某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直
某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com