
分析 设O′、O分别是上、下底面的中心,连结OO′、O′B′、OB,在平面BCC′B′内过B′作B′D⊥BC于D,在平面BOO′B′内作B′E⊥OB于E,求出棱台高为$\frac{\sqrt{42}}{3}$cm,梯形有高为$\sqrt{5}$,由此能求出该三棱台的侧面积和体积.
解答 (本小题满分12分)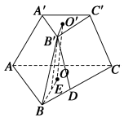
解:如图所示,O′、O分别是上、下底面的中心,
连结OO′、O′B′、OB,
在平面BCC′B′内过B′作B′D⊥BC于D,
在平面BOO′B′内作B′E⊥OB于E,
∵△A′B′C′是边长为2的等边三角形,O′是中心,
∴O′B′=$\frac{2}{3}×2×\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}$,
在Rt△B′EB中,$B{B}^{'}=\sqrt{6}$,BE=$\frac{2\sqrt{3}}{3}$,
∴B′E=$\frac{\sqrt{42}}{3}$,即棱台高为$\frac{\sqrt{42}}{3}$cm,
∴三棱台的体积为:
${V}_{棱台}=\frac{1}{3}×\frac{\sqrt{42}}{3}(\frac{\sqrt{3}}{4}×16+\frac{\sqrt{3}}{4}×4+\sqrt{\frac{\sqrt{3}}{4}×16×\frac{\sqrt{3}}{4}×4})$=$\frac{7\sqrt{14}}{3}$(cm3).
∵棱台的侧面是等腰梯形,
∴BD=$\frac{1}{2}(4-2)=1$,
在Rt△B′DB中,BB′=$\sqrt{6}$,BD=1,
∴B′D=$\sqrt{5}$,即梯形有高为$\sqrt{5}$,
∴该三棱台的侧面积S侧=3×$\frac{1}{2}×(2+4)×\sqrt{5}$=9$\sqrt{5}$(cm2).
该三棱台的侧面积为$9\sqrt{5}$cm2,体积为$\frac{7}{3}\sqrt{14}$cm3.
点评 本解决棱锥、棱台的侧面积、表面积及体积问题时,往往将已知条件归结到一个直角三角形中求解,为此在解此类问题时,要注意直角三角形的应用.


科目:高中数学 来源: 题型:填空题
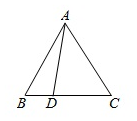 如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.
如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a$?$\overrightarrow b$=$\overrightarrow b$?$\overrightarrow a$ | B. | (k$\overrightarrow a$)?$\overrightarrow b$=$\overrightarrow a$?(k$\overrightarrow b$) | C. | $\overrightarrow a$•($\overrightarrow b$?$\overrightarrow c$)=$\overrightarrow b$•($\overrightarrow a$?$\overrightarrow c$) | D. | |$\overrightarrow a$?$\overrightarrow b$|=$\frac{|\overrightarrow a•\overrightarrow b|}{\overrightarrow b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x3 | C. | f(x)=-x2 | D. | f(x)=-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com