
| A. | $\overrightarrow a$?$\overrightarrow b$=$\overrightarrow b$?$\overrightarrow a$ | B. | (k$\overrightarrow a$)?$\overrightarrow b$=$\overrightarrow a$?(k$\overrightarrow b$) | C. | $\overrightarrow a$•($\overrightarrow b$?$\overrightarrow c$)=$\overrightarrow b$•($\overrightarrow a$?$\overrightarrow c$) | D. | |$\overrightarrow a$?$\overrightarrow b$|=$\frac{|\overrightarrow a•\overrightarrow b|}{\overrightarrow b}$ |
分析 根据定义,$\overrightarrow a$?$\overrightarrow b$=$\overrightarrow a$cosθ,$\overrightarrow a$,$\overrightarrow c$的夹角为α,$\overrightarrow b$,$\overrightarrow c$的夹角为β,根据新定义逐一判断即可
解答 解:根据定义,$\overrightarrow a$?$\overrightarrow b$=$\overrightarrow a$cosθ,$\overrightarrow a$,$\overrightarrow c$的夹角为α,$\overrightarrow b$,$\overrightarrow c$的夹角为β,
对于A,$\overrightarrow a$?$\overrightarrow b$=$\overrightarrow{a}$cosθ,$\overrightarrow{b}$?$\overrightarrow{a}$=$\overrightarrow{b}$cosθ,二者不一定相等;
对于B,(k$\overrightarrow{a}$)?$\overrightarrow{b}$=k$\overrightarrow{a}$cosθ,$\overrightarrow{a}$?(k$\overrightarrow{b}$)=$\overrightarrow{a}$cosθ,二者不一定相等;
对于C,$\overrightarrow{a}$•($\overrightarrow{b}$?$\overrightarrow{c}$)=$\overrightarrow{a}$•($\overrightarrow{c}$cosβ)=|$\overrightarrow{a}$|×|$\overrightarrow{c}$|cosαcosβ,
$\overrightarrow{b}$•($\overrightarrow{a}$?$\overrightarrow{c}$)=$\overrightarrow{b}$•$\overrightarrow{c}$cosα=|$\overrightarrow{b}$|×|$\overrightarrow{c}$|cosβcosα,二者不一定相等;
对于D,|$\overrightarrow{a}$?$\overrightarrow{b}$|=|$\overrightarrow{b}$cosθ|=|$\overrightarrow{b}$|×|cosθ|=$\frac{|\overrightarrow{a}•\overrightarrow{b}|}{\overrightarrow{b}}$.
故选:D
点评 本题考查了一种新定义向量运算“?”、向量共线定理、数量积运算等基础知识,考查了分类讨论思想方法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
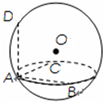 如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.
如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|y≥0} | B. | {x|x$>\frac{1}{2}$} | C. | {x|0$<x<\frac{1}{2}$} | D. | {y|y>0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)>f($\frac{\sqrt{3}}{3}$) | B. | f($\sqrt{2}$)>f(-$\sqrt{2}$) | C. | f(4)>f(3) | D. | f(-$\sqrt{2}$)>f($\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com