
【题目】已知命题![]() :关于
:关于![]() 的不等式
的不等式![]() 无解;命题
无解;命题![]() :指数函数
:指数函数![]() 是增函数.
是增函数.
(1)若命题![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)若满足![]() 为假命题
为假命题![]() 为真命题的实数
为真命题的实数![]() 取值范围是集合
取值范围是集合![]() ,集合
,集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)[4,+∞) (2)[-3,2]
【解析】
(1)根据题干条件得到命题p下的m的范围,和命题q下m的范围,两者取交集即可;(2)由(1)可知,m的取值范围是(3,4)即A={m|3<m<4},根据集合间的包含关系得到不等式组,解出即可.
(1)由p为真命题知, =16-4m≤0解得m≥4,所以m的范围是[4,+∞),
由q为真命题知,2m-5>1,m>3,取交集得到[4,+∞).
综上, m的范围是[4,+∞)。
(2)由(1)可知,当p为假命题时,m<4; q为真命题,则2m-5>1解得:m>3
则,m的取值范围是(3,4)即A={m|3<m<4},
而AB,可得,![]()
解得:-3≤t≤2.
所以,t的取值范围是[-3,2]


科目:高中数学 来源: 题型:
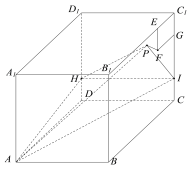
【题目】如图所示,正方体ABCD﹣A1B1C1D1棱长为4,点![]() 在棱
在棱![]() 上,点
上,点![]() 在棱
在棱![]() 上,且
上,且![]() .在侧面
.在侧面![]() 内以
内以![]() 为一个顶点作边长为1的正方形
为一个顶点作边长为1的正方形![]() ,侧面
,侧面![]() 内动点
内动点![]() 满足到平面
满足到平面![]() 距离等于线段
距离等于线段![]() 长的
长的![]() 倍,则当点
倍,则当点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积的最小值是( )
的体积的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间![]() 上的两个函数
上的两个函数![]() 和
和![]() ,如果对任意的
,如果对任意的![]() ,均有不等式
,均有不等式![]() 成立,则称函数
成立,则称函数![]() 与
与![]() 在
在![]() 上是“友好”的,否则称为“不友好”的.
上是“友好”的,否则称为“不友好”的.
(1)若![]() ,
,![]() ,则
,则![]() 与
与![]() 在区间
在区间![]() 上是否“友好”;
上是否“友好”;
(2)现在有两个函数![]() 与
与![]() ,给定区间
,给定区间![]() .
.
①若![]() 与
与![]() 在区间
在区间![]() 上都有意义,求
上都有意义,求![]() 的取值范围;
的取值范围;
②讨论函数![]() 与
与![]() 与在区间
与在区间![]() 上是否“友好”.
上是否“友好”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() ,直线
,直线![]() 过定点
过定点![]() .
.
(1)若![]() 与圆相切,求
与圆相切,求![]() 的方程;
的方程;
(2)若![]() 与圆相交于
与圆相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,又
,又![]() 与
与![]() 的交点为
的交点为![]() ,判断
,判断![]() 是否为定值.若是,求出定值;若不是,请说明理由.
是否为定值.若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下说法:
①一年按365天计算,两名学生的生日相同的概率是![]() ;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com