
分析 先根据抛物线方程求得焦点坐标及准线方程,进而根据抛物线的定义可知点P到焦点的距离与到准线的距离相等,进而推断出yp+1=6,求得yp,代入抛物线方程即可求得点P的横坐标,则点P的坐标可得.
解答 解:根据抛物线方程可求得焦点坐标为(0,1),准线方程为y=-1,
根据抛物线定义,∴yp+1=6,
解得yp=5,代入抛物线方程求得x=±2$\sqrt{5}$
∴P点坐标是$(2\sqrt{5},5),(-2\sqrt{5},5)$.
故答案为:$(2\sqrt{5},5),(-2\sqrt{5},5)$.
点评 本题主要考查抛物线的定义:抛物线上的点到焦点距离与到准线距离相等,常可用来解决涉及抛物线焦点的直线或焦点弦的问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
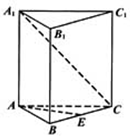 如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[0,2\sqrt{2}]$ | B. | $[0,\sqrt{2}]$ | C. | [1,2] | D. | $[\sqrt{2},2\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设A,B分比为椭圆E$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,P是椭圆E上不同于A,B的一动点,点F是椭圆E的右焦点,直线l是椭圆E的右准线,若直线AP与直线:x=a和l分别相较于C,Q两点,FQ与直线BC交于M.
如图,设A,B分比为椭圆E$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,P是椭圆E上不同于A,B的一动点,点F是椭圆E的右焦点,直线l是椭圆E的右准线,若直线AP与直线:x=a和l分别相较于C,Q两点,FQ与直线BC交于M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com