
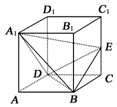
 如图所示,在正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.
如图所示,在正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.分析 (1)连接AC,设AC∩DB=O,连接A1O,OE.证明A1A⊥BD,BD⊥AC,推出BD⊥平面ACEA1,然后证明A1E⊥BD.
(2)当E是CC1的中点时,平面A1BD⊥平面EBD.说明∠A1OE为二面角A1-BD-E的平面角.设棱长为2a,推出∠A1OE=90°.即可证明平面A1BD⊥平面EBD.
解答 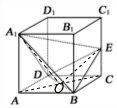 解:连接AC,设AC∩DB=O,连接A1O,OE.
解:连接AC,设AC∩DB=O,连接A1O,OE.
(1)∵A1A⊥底面ABCD,∴A1A⊥BD,又BD⊥AC,
∴BD⊥平面ACEA1,∵A1E?平面ACEA1,
∴A1E⊥BD.
(2)证明:当E是CC1的中点时,平面A1BD⊥平面EBD.
证明如下:
∵A1B=A1D,EB=ED,O为BD中点,∴A1O⊥BD,EO⊥BD
∴∠A1OE为二面角A1-BD-E的平面角.
在正方体ABCD-A1B1C1D1中,设棱长为2a,
∵E为棱CC1的中点,由平面几何知识,EO=$\sqrt{3}$a,A1O=$\sqrt{6}$a,A1E=3a,
∴A1E2=A1O2+EO2,即∠A1OE=90°.
∴平面A1BD⊥平面EBD.
点评 本题考查直线与直线垂直,直线与平面垂直的判定定理以及性质定理的应用,二面角的平面角的求法,平面与平面垂直的证明方法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
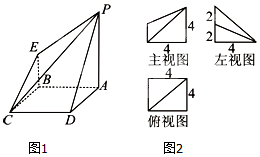 如图是一几何体的直观图、主观图、俯视图、左视图.
如图是一几何体的直观图、主观图、俯视图、左视图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
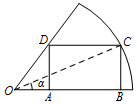 为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.
为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com