
【题目】函数f(x)=( ![]() )x﹣(
)x﹣( ![]() )x﹣1+2(x∈[﹣2,1])的值域是( )
)x﹣1+2(x∈[﹣2,1])的值域是( )
A.( ![]() ,10]
,10]
B.[1,10]
C.[1, ![]() ]
]
D.[ ![]() ,10]
,10]
【答案】B
【解析】解:令t=( ![]() )x(x∈[﹣2,1]),
)x(x∈[﹣2,1]),
则t∈[ ![]() ,4],
,4],
f(x)=g(t)=t2﹣2t+2(t∈[ ![]() ,4]),
,4]),
由g(t)=t2﹣2t+2的图象是开口朝上,且以直线t=1为对称轴的抛物线,
故当t=1时,函数取最小值1,
当t=4时,函数取最大值10,
故函数的值域为[1,10],
故选:B
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,以及对函数的最值及其几何意义的理解,了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1 , BD的中点. 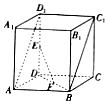
(1)求证:EF∥平面ABC1D1;
(2)AA1=2 ![]() ,求异面直线EF与BC所成的角的大小.
,求异面直线EF与BC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点,![]() 为原点,
为原点,![]()
![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(ax2﹣4x+a)(a∈R),若f(x)的值域为R,则实数a的取值范围是( )
A.[0,2]
B.(2,+∞)
C.(0,2]
D.(﹣2,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>b>1,若logab+logba= ![]() ,ab=ba , 则由a,b,3b,b2 , a﹣2b构成的包含元素最多的集合的子集个数是( )
,ab=ba , 则由a,b,3b,b2 , a﹣2b构成的包含元素最多的集合的子集个数是( )
A.32
B.16
C.8
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,己知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( ) 
A.﹣ ![]()
B.![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com