
分析 (1)由$\overrightarrow{m}⊥\overrightarrow{n}$便得到$\overrightarrow{m}•\overrightarrow{n}=0$,进行数量积的坐标运算便可得到cosB=$\frac{1}{2}$,从而得出B=$\frac{π}{3}$;
(2)根据余弦定理便有b2=a2+c2-2accosB,这样即可求出b的值.
解答 解:(1)∵$\overrightarrow{m}⊥\overrightarrow{n}$;
∴$\overrightarrow{m}•\overrightarrow{n}=0$;
即2cosB(1-sinB)+sin2B-1=2cosB-2sinBcosB+sin2B-1=2cosB-1=0;
∴$cosB=\frac{1}{2}$;
又B∈(0,π);
∴$B=\frac{π}{3}$;
(2)在△ABC中,$a=1,c=2,B=\frac{π}{3}$;
∴由余弦定理得,${b}^{2}={a}^{2}+{c}^{2}-2accos\frac{π}{3}$=1+4-2=3;
∴$b=\sqrt{3}$.
点评 考查向量垂直的充要条件,向量数量积的坐标运算,二倍角的正弦公式,已知三角函数值求角,以及余弦定理.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
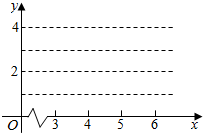 某厂通过技术改造降低了产品A对重要原材料G的消耗,如表提供了该厂技术改造后生产产品A的过程记录的产量x(吨)与原材料G相应的消耗量y(吨)的几组对照数据:
某厂通过技术改造降低了产品A对重要原材料G的消耗,如表提供了该厂技术改造后生产产品A的过程记录的产量x(吨)与原材料G相应的消耗量y(吨)的几组对照数据:| x | 3 | 4 | 5 | 6 |
| y | 1.6 | 2.2 | 3.0 | 3.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
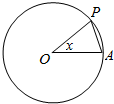 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )| A. | 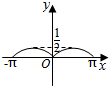 | B. | 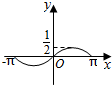 | C. |  | D. | 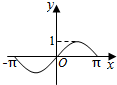 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨¬q | B. | ¬p∧q | C. | ¬q∧¬q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -300 | B. | -150 | C. | 150 | D. | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com