
分析 (1)根据绝对值不等式的解法,利用分类讨论的思想进行求解即可.
(2)利用基本不等式,结合绝对值的性质进行证明即可.
解答 解:(1)由f(x)<2+|x+1|得|x-3|<2+|x+1|,
即|x-3|-|x+1|<2,
即当x<-1时,不等式等价为-x+3+x+1<2,即4<2,此时不等式无解,
当-1≤x≤3时,不等式等价为-x+3-x-1<2,即-2x+2<2,得x>0,此时0<x≤3,
当x>3时,不等式等价为x-3-x-1<2,即-4<2,成立,此时x>3,
综上不等式的解为x>0,
即不等式的解集为(0,+∞);
(2)已知m,n∈R+且$\frac{1}{m}$+$\frac{1}{n}$=2mn,
∴2mn≥2$\sqrt{\frac{1}{m}•\frac{1}{n}}$=$\frac{2}{\sqrt{mn}}$,
则mn≥1,
则mf(n)+nf(-m)=m|n-3|+n|-m-3|=|mn-3n|+|mn+3n|≥|(mn-3n-(mn+3m)|=3|m+n|≥6$\sqrt{mn}$≥6.
点评 本题主要考查绝对值不等式的解法和证明,利用分类讨论的思想结合绝对值的性质是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 日 期 | 3月21日 | 3月22日 | 3月23日 | 3月24日 | 3月25日 |
| 平均气温x(°C) | 8 | 10 | 14 | 11 | 12 |
| 销量y(杯) | 21 | 25 | 35 | 26 | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M={(1,2)},N={(2,1)} | B. | M={1,2},N={(2,1)} | ||
| C. | M=∅,N={∅} | D. | M={x︳x2-3x+2=0},N={1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 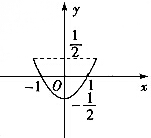 | B. | 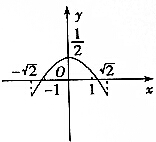 | ||
| C. | 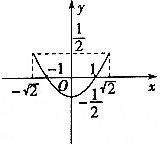 | D. | 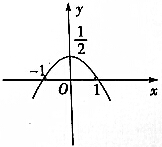 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{24}{7}$ | B. | $\frac{24}{7}$ | C. | -$\frac{7}{24}$ | D. | $\frac{7}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{7}{6}$ | D. | $\frac{7}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com