
| A. | 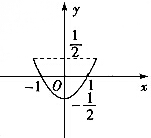 | B. | 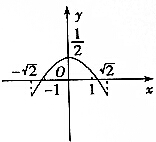 | ||
| C. | 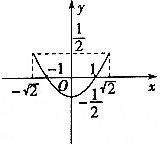 | D. | 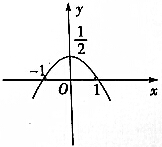 |
分析 对x=sinθ+cosθ两边平方,得出曲线的普通方程,判断抛物线的开口方向,根据三角恒等变换判断x的取值范围.
解答 解:∵$\left\{\begin{array}{l}{x=sinθ+cosθ}\\{y=sinθcosθ}\end{array}\right.$(θ为参数),∴x2=sin2θ+2sinθcosθ+cos2θ=1+2sinθcosθ=1+2y=2(y+$\frac{1}{2}$).
∴曲线表示开口向上的抛物线.
又∵x=sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),∴-$\sqrt{2}≤x≤\sqrt{2}$.
故选:C.
点评 本题考查了参数方程与普通方程的互化,属于基础题,注意x,y的取值范围是需要注意的地方.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
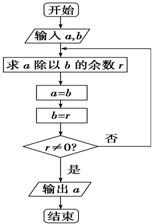 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com