
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{π}{3}$,$\frac{4π}{3}$] | C. | [$\frac{π}{3}$,π] | D. | [0,π] |
分析 由α∈[0,2π],可得范围$α-\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{5π}{3}$],由已知利用两角差的正弦函数公式可得sin($α-\frac{π}{3}$)≥0,利用正弦函数的图象可得:0≤$α-\frac{π}{3}$≤π,即可得解.
解答 解:∵α∈[0,2π],
∴$α-\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{5π}{3}$],
∵sinα≥$\sqrt{3}$cosα,
∴sinα-$\sqrt{3}$cosα≥0,可得:2sin($α-\frac{π}{3}$)≥0,即sin($α-\frac{π}{3}$)≥0,
∴利用正弦函数的图象可得:0≤$α-\frac{π}{3}$≤π,
∴解得:α∈[$\frac{π}{3}$,$\frac{4π}{3}$],
故选:B.
点评 本题主要考查了两角差的正弦函数公式,正弦函数的图象和性质,考查了数形结合的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
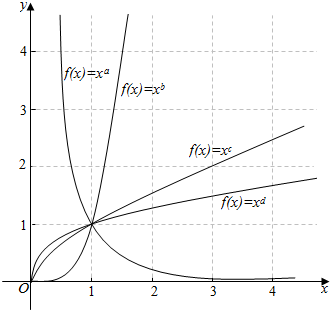
| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
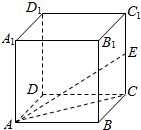
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③④ | B. | ①②④ | C. | ①④ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
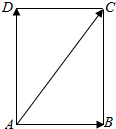 一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.
一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+$\frac{16}{x}$ | B. | x2+$\frac{16}{x}$ | C. | x+$\frac{32}{{x}^{2}}$ | D. | x+$\frac{36}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com