
分析 分别画出函数的图象,由函数零点存在定理即可判断.
解答 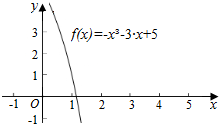 解:(1)∵函数f(x)=-x3-3x+5是单调递减函数,
解:(1)∵函数f(x)=-x3-3x+5是单调递减函数,
又∵f(1)=-13-3×1+5=1>0,f(2)=-23-3×2+5=-9<0,
∴函数f(x)的零点必在区间(1,2)上,
故必存在零点的区间是 (1,2),图象如图所示:
(2)∵函数f(x)=2x•ln(x-2)-3是单调递增函数,
又∵f(4)=8ln2-3>0,f(3)=-3<0,
∴函数f(x)的零点必在区间(3,4)上,
故必存在零点的区间是 (3,4),图象如图所示: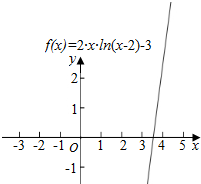
(3)∵函数f(x)=ex-1+4x-4是单调递增函数,
又∵f(1)=1+4-4>0,f(0)=$\frac{1}{e}$-4<0,
∴函数f(x)的零点必在区间(0,1)上,
故必存在零点的区间是 (0,1),图象如图所示: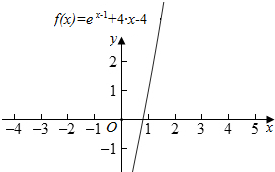
(4)f(x)=3(x+2)(x-3)(x+4)+x的图象如图所示,
∵f(-4)=-4<0,f(-3)=15>0,f(-2)=-2<0,f(3)=3>0,f(2)<0,
∴函数f(x)的零点在区间(-4,3),(-3,-2),(2,3)上.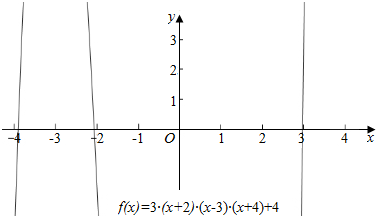
点评 本题考查函数的零点存在的条件:单调的连续函数若在一个区间的端点的函数值异号,则函数在此区间上一定存在零点.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
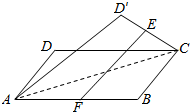 设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )
设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )| A. | $\frac{3\sqrt{5}}{16}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{51}}{17}$ | D. | $\frac{\sqrt{57}}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{π}{3}$,$\frac{4π}{3}$] | C. | [$\frac{π}{3}$,π] | D. | [0,π] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100$\sqrt{2}$米 | B. | 120$\sqrt{2}$米 | C. | 150$\sqrt{3}$米 | D. | 150$\sqrt{2}$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com