
分析 (Ⅰ)直接根据抛物线的定义即可求出抛物线C的焦点坐标和准线方程;
(Ⅱ)由题意,知直线l的斜率存在,故设l的方程为y=kx+m,构造方程组,根据根与系数关系和导数的几何意义得到抛物线在点A,B处的切线方程,得到x=$\frac{1}{2}$(x1+x2),代入即可证明;
(Ⅲ)假设存在点P,使得四边形PEQF为矩形,由四边形PEQF为矩形,得EQ⊥FQ,AQ⊥BQ,根据直线的斜率得到P(0,1),再利用斜率相等验证PEQF为平行四边形即可.
解答 (Ⅰ)解:焦点坐标为(0,1),准线方程为Y=-1.…(2分)
(Ⅱ)证明:由题意,知直线l的斜率存在,故设l的方程为y=kx+m.
由方程组$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}=4y}\end{array}\right.$ 得x2-4kx-4m=0,
由题意,得△=16k2+16m>0.
设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4m,…(4分)
由抛物线方程x2=4y,得y=$\frac{1}{4}$x2,所以y′=$\frac{1}{2}$x,
所以抛物线在点A处的切线方程为y-$\frac{1}{4}{x}_{1}^{2}$=$\frac{1}{2}$x1(x-x1),
化简,得y=$\frac{1}{2}$x1x-$\frac{1}{4}{x}_{1}^{2}$
同理,抛物线在点B处的切线方程为y=$\frac{1}{2}$x2x-$\frac{1}{4}{x}_{2}^{2}$ …(6分)
联立方程,得$\frac{1}{2}$x1x-$\frac{1}{4}{x}_{1}^{2}$=$\frac{1}{2}$x2x-$\frac{1}{4}{x}_{2}^{2}$
即$\frac{1}{2}$(x1-x2)x=$\frac{1}{4}$(x1-x2)(x1+x2),
因为x1≠x1,所以x=$\frac{1}{2}$(x1+x2),
代入,得y=$\frac{1}{4}$x1x2=-m,
所以点Q($\frac{1}{2}$(x1+x2),-m),即Q(2k,-m)
点Q在直线y=-m上.…(8分)
(Ⅲ)解:假设存在点P,使得四边形PEQF为矩形,
由四边形PEQF为矩形,得EQ⊥FQ,AQ⊥BQ
∴kAQ•kBQ=-1,$\frac{1}{2}$x1$•\frac{1}{2}$x2=-1,
∴$\frac{1}{4}$x1x2=$\frac{1}{4}$(-4m)=-1,
∴m=1,P(0,1)
下面验证此时的四边形PEQF为平行四边形即可.
令y=0,得E($\frac{1}{2}$x1,0).
同理得F($\frac{1}{2}$x2,0).
所以直线EP的斜率为kEP=$\frac{1-0}{0-\frac{1}{2}{x}_{1}}$=$\frac{-2}{{x}_{1}}$,
直线FQ的斜率kFQ=$\frac{0-(-1)}{\frac{1}{2}{x}_{2}-\frac{{x}_{1}+{x}_{2}}{2}}$=$\frac{-2}{{x}_{1}}$,…(12分)
所以kEP=kFQ,即EP∥FQ.
同理PF∥EQ.所以四边形PEQF为平行四边形.
综上所述,存在点P(0,1),使得四边形PEQF为矩形.…(14分)
点评 本题考查直线、抛物线等基础知识,考查直线与抛物线的位置关系,考查运算求解能力,抽象思维能力,考查数形结合思想,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
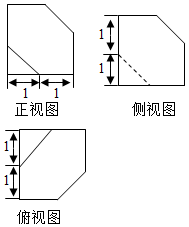
| A. | 4 | B. | 3$\sqrt{3}$+12 | C. | 21+$\sqrt{3}$ | D. | $\frac{{3\sqrt{3}}}{2}$+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com