
 如图,已知△ABC的等腰直角三角形,CA=1,点P是△ABC内一点,过点P分别引三边的平行线,与各边围成以P为顶点的三个三角形(图中阴影部分).当点P在△ABC内运动时,以P为顶点的三个三角形面积的最小值为$\frac{1}{6}$.
如图,已知△ABC的等腰直角三角形,CA=1,点P是△ABC内一点,过点P分别引三边的平行线,与各边围成以P为顶点的三个三角形(图中阴影部分).当点P在△ABC内运动时,以P为顶点的三个三角形面积的最小值为$\frac{1}{6}$. 分析 以C为原点,CA所在直线为x轴,CB所在直线为y轴,建立平面直角坐标系,再设过点P且平行于直线AB的直线方程为x+y=a,(0<a<1),设点P(m,a-m),从而表示出边长进而表示出面积,从而利用二次函数求最小值即可.
解答  解:如图,以C为原点,CA所在直线为x轴,CB所在直线为y轴,建立平面直角坐标系,
解:如图,以C为原点,CA所在直线为x轴,CB所在直线为y轴,建立平面直角坐标系,
则C(0,0),A(1,0),B(0,1);
设过点P且平行于直线AB的直线方程为x+y=a,(0<a<1)
设点P(m,a-m),
则MP=HM=m,PD=ED=a-m,GP=PF=1-a;
故S=$\frac{1}{2}$m2+$\frac{1}{2}$(a-m)2+$\frac{1}{2}$(1-a)2
=(m-$\frac{a}{2}$)2+$\frac{3}{4}$a2-a+$\frac{1}{2}$
≥$\frac{3}{4}$a2-a+$\frac{1}{2}$
=$\frac{3}{4}$(a-$\frac{2}{3}$)2+$\frac{1}{6}$≥$\frac{1}{6}$;
(当a=$\frac{2}{3}$,m=$\frac{1}{3}$时,等号成立)
故答案为:$\frac{1}{6}$.
点评 本题考查了函数在实际问题中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
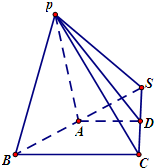 在三棱锥P-SBC中,A,D分别为边SB,SC的中点,AB=2,BC=4,CD=2$\sqrt{2}$.平面PSB⊥平面ABCD,平面PAD⊥平面ABCD.
在三棱锥P-SBC中,A,D分别为边SB,SC的中点,AB=2,BC=4,CD=2$\sqrt{2}$.平面PSB⊥平面ABCD,平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,△PAB是正三角形,四边形ABCD是矩形,且面PAB⊥面ABCD,PA=1,PC=2.
如图,四棱锥P-ABCD中,△PAB是正三角形,四边形ABCD是矩形,且面PAB⊥面ABCD,PA=1,PC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com