
【题目】在直角梯形PBCD中,∠D=∠C![]() ,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
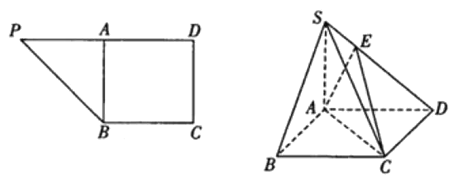
(1)求证:SA⊥平面ABCD;
(2)若E为SD中点,求D点到面EAC的距离.
【答案】(1)见解析 (2)![]()
【解析】
(1)先证明BC⊥平面SAB,得到BC⊥SA,结合SA⊥AB,即得证;
(2)D点到面EAC的距离即为三棱锥![]() 以平面
以平面![]() 为底面的高,利用等体积法:
为底面的高,利用等体积法:![]() 即得解.
即得解.
(1)证明:在直角梯形PBCD中,由题意得BA⊥PD,ABCD是正方形,
∴在翻折后的图形中,SA⊥AB,SA=2,四边形ABCD是边长为2的正方形,
∵SB⊥BC,AB⊥BC,SB∩AB=B,∴BC⊥平面SAB,
∵SA平面SAB,∴BC⊥SA,
∵SA⊥AB,BC∩AB=B,∴SA⊥平面ABCD.
(2)D点到面EAC的距离即为三棱锥![]() 以平面
以平面![]() 为底面的高,
为底面的高,
利用等体积法:![]()
即:![]()
由于E为SD中点,故![]() ,
,![]()
由于![]() 为等腰直角三角形,且E为SD中点,故
为等腰直角三角形,且E为SD中点,故![]()
由于SA⊥平面ABCD,故SA⊥CD,且AD⊥CD, SA∩AD=A
∴CD⊥平面SAD,∵SD平面SAD,∴CD⊥SD
故![]() 为直角三角形,故
为直角三角形,故![]() ,又
,又![]()
![]()
![]()
故: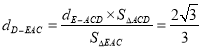


科目:高中数学 来源: 题型:
【题目】某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是 ![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() .
.
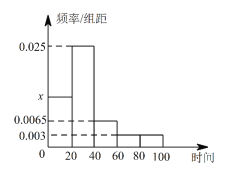
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)如果年上缴税收不少于![]() 万元的企业可申请政策优惠,若共抽取企业
万元的企业可申请政策优惠,若共抽取企业![]() 个,试估计有多少企业可以申请政策优惠;
个,试估计有多少企业可以申请政策优惠;
(Ⅲ)从企业中任选![]() 个,这
个,这![]() 个企业年上缴税收少于
个企业年上缴税收少于![]() 万元的个数记为
万元的个数记为 ![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.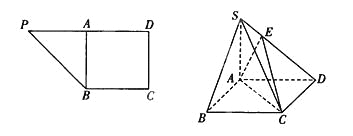
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同类班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)
优秀人数 | 非优秀人数 | 总计 | |
甲班 |
|
|
|
乙班 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 把握认为加强语文阅读训练与提高数学应用题得分率有关?
把握认为加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在![]() 分钟,小刚正确解答一道数学应用题所用的时间在
分钟,小刚正确解答一道数学应用题所用的时间在![]() 分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
(3)现从乙班成绩优秀的![]() 名同学中任意抽取两人,并对他们的答题情况进行全程研究,记
名同学中任意抽取两人,并对他们的答题情况进行全程研究,记![]() 两人中被抽到的人数为
两人中被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
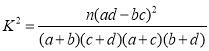
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】邗江中学高二年级某班某小组共10人,利用寒假参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中选出2人作为该组代表参加座谈会.
(1)记“选出2人参加义工活动的次数之和为4”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出2人参加义工活动次数之差的绝对值,求随机变量
为选出2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() .记过
.记过![]() 、
、![]() 、
、![]() 三点的圆为圆
三点的圆为圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求过点![]() 与圆
与圆![]() 相交所得弦长为
相交所得弦长为![]() 的直线方程.
的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com