
分析 (I)曲线C的极坐标方程为:ρsin2θ=cosθ,即ρ2sin2θ=ρcosθ,化为直角坐标方程:y2=x,通过变换可得曲线C1的方程.
(II)直线l的极坐标方程为$\sqrt{2}ρcos(θ-\frac{π}{4})-2=0$,展开可得:$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)-2=0,利用互化公式可得直角坐标方程.可得参数方程:$\left\{\begin{array}{l}{x=2-\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),代入曲线C1的直角坐标方程可得:t2+2$\sqrt{2}$t-4=0,利用|PA|+|PB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$即可得出.
解答 解:(I)曲线C的极坐标方程为:ρsin2θ=cosθ,即ρ2sin2θ=ρcosθ,化为直角坐标方程:y2=x.
将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1:y2=2(x-1).
(II)直线l的极坐标方程为$\sqrt{2}ρcos(θ-\frac{π}{4})-2=0$,展开可得:$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)-2=0,可得直角坐标方程:x+y-2=0.
可得参数方程:$\left\{\begin{array}{l}{x=2-\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数).
代入曲线C1的直角坐标方程可得:t2+2$\sqrt{2}$t-4=0.
解得t1+t2=-2$\sqrt{2}$,t1•t2=-4..
∴|PA|+|PB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{(-2\sqrt{2})^{2}-4×(-4)}$=$2\sqrt{6}$.
点评 本题考查了极坐标方程与直角坐标方程的互化、直线参数方程及其应用、相交弦长公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. |  | B. | 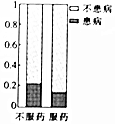 | C. | 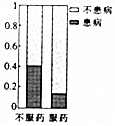 | D. | 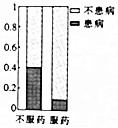 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
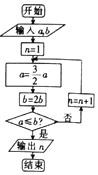 名著《算学启蒙》中有如下题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”.这段话的意思是:“松有五尺长,竹有两尺长,松每天增长前一天长度的一半,竹每天增长前一天长度的两倍.”.为了研究这个问题,以a代表松长,以b代表竹长,设计了如图所示的程序框图,输入的a,b的值分别为5,2,则输出的n的值为( )
名著《算学启蒙》中有如下题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”.这段话的意思是:“松有五尺长,竹有两尺长,松每天增长前一天长度的一半,竹每天增长前一天长度的两倍.”.为了研究这个问题,以a代表松长,以b代表竹长,设计了如图所示的程序框图,输入的a,b的值分别为5,2,则输出的n的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3}{4}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sinx | B. | f(x)=|x+1| | C. | f(x)=-x | D. | f(x)=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com