Question

18．在区间[1，e]上任取实数a，在区间[0，1]上任取实数b，使函数f（x）=ax²+x+$\frac{1}{4}$b有两个相异零点的概率是（　　）

• A． $\frac{1}{e-1}$
• B． $\frac{1}{2（e-1）}$
• C． $\frac{1}{4（e-1）}$
• D． $\frac{1}{8（e-1）}$

Answer 1

分析 首先求出在区间[1，e]上任取实数a，在区间[0，1]上任取实数b，使函数f（x）=ax²+x+$\frac{1}{4}$b有两个相异零点的a，b关系，利用区域的面积比求概率．

解答 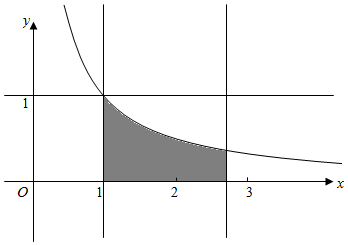解：在区间[1，e]上任取实数a，
在区间[0，1]上任取实数b，对应区域是边长分别为e-1，1的矩形，面积为e-1，而使函数f（x）=ax²+x+$\frac{1}{4}$b有两个相异零点的a，b满足$\left\{\begin{array}{l}{1≤a≤e}\\{0≤b≤1}\\{△=1-ab＞0}\end{array}\right.$，对应区域如图阴影部分：由几何概型的公式得到所求概率为$\frac{{∫}_{1}^{e}\frac{1}{a}da}{e-1}=\frac{lne}{e-1}=\frac{1}{e-1}$；
故选A．

点评 本题考查了几何概型的概率求法；关键是明确几何测度为对应区域的面积，利用数形结合理解概率为对应区域的面积比．