
| A. | (-∞,$\frac{1}{8}$] | B. | (0,$\frac{1}{8}$] | C. | (0,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,+∞) |
分析 依题意知直线ax-by+1=0过圆C的圆心(-1,2),故有a+2b=1,再利用ab=(1-2b)b=-2(b-$\frac{1}{4}$)2+$\frac{1}{8}$≤$\frac{1}{8}$,求得ab的取值范围.
解答 解:∵直线ax-by+1=0平分圆C:x2+y2+2x-4y+1=0的周长,
∴直线ax-by+1=0过圆C的圆心(-1,2),
∴有a+2b=1,
∴ab=(1-2b)b=-2(b-$\frac{1}{4}$)2+$\frac{1}{8}$≤$\frac{1}{8}$,
∵a>0,b>0,
∴ab的取值范围是(0,$\frac{1}{8}$].
故选:B.
点评 本题主要考查直线和圆的位置关系,配方法的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
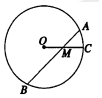 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )| A. | 2cm | B. | 8cm | C. | 10cm | D. | 12cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,2] | B. | [-7,-6] | C. | [-9,-4] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | y=1 | C. | y-1=$\sqrt{2}$(x+1) | D. | y-1=2$\sqrt{2}$(x+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{1+\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.
为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com