Question

10．若不等式|a-2x|≤x+3对任意x∈[0，2]恒成立，则实数a的取值范围是（　　）

• A． （-1，3）
• B． [-1，3]
• C． （1，3）
• D． [1，3]

Answer 1

分析 由题意可得f（x）=|a-2x|的图象在x∈[0，2]上恒位于直线y=x+3的下方或在直线y=x+3上，数形结合可得$\left\{\begin{array}{l}{\frac{a}{2}＜0}\\{f（2）=|4-a|≤5}\end{array}\right.$ ①，或 $\left\{\begin{array}{l}{\frac{a}{2}≥0}\\{f（2）=|a-4|≤5}\\{f（0）=|a|≤3}\end{array}\right.$ ②，分别求得①、②的解集，再取并集，即得所求．

解答 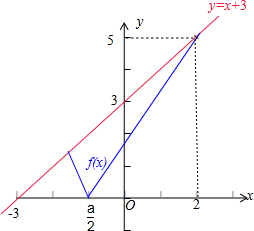解：由不等式|a-2x|≤x+3对任意x∈[0，2]上恒成立，
可得f（x）=|a-2x|的图象在x∈[0，2]上恒位于直线y=x+3的下方或在直线y=x+3上，
如图所示：
∴$\left\{\begin{array}{l}{\frac{a}{2}＜0}\\{f（2）=|4-a|≤5}\end{array}\right.$ ①，或 $\left\{\begin{array}{l}{\frac{a}{2}≥0}\\{f（2）=|a-4|≤5}\\{f（0）=|a|≤3}\end{array}\right.$ ②．
由①可得-1≤a＜0，由②可得0≤a≤3，
故实数a的取值范围是{a|-1≤a＜0，或者0≤a≤3}=[-1，3]，
故选：B．

点评 本题主要考查绝对值不等式的解法，函数的恒成立问题，体现了数形结合、分类讨论的数学思想，属于中档题．