Question

1．在直角坐标系中划出下列方程表示的图象
（1）x²+2xy-3y²=0；（2）$\sqrt{{x}^{2}-4}$•$\sqrt{y+2}$=0；（3）|x|+|y|=1．

Answer 1

分析 （1）由因式分解可得（x+3y）（x-y）=0，可得图象为两条直线；
（2）方程等价为x²-4=0或y=-2，图象为三条直线；
（3）讨论x，y的符号，可得图象为四条线段构成的正方形．

解答 解：（1）x²+2xy-3y²=0，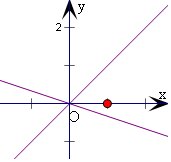
即为（x+3y）（x-y）=0，
即x=y或x=-3y，
图象如右图两条直线；
（2）$\sqrt{{x}^{2}-4}$•$\sqrt{y+2}$=0，
即为x²-4=0或y=-2，
即有x=±2，或y=-2，
图象如右下图三条直线；
（3）|x|+|y|=1，
当x≥0，y≥0时，可得x+y=1；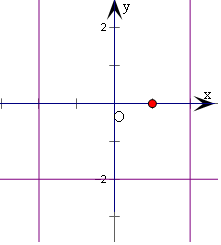
当x≤0，y≤0时，可得-x-y=1；
当x≥0，y≤0时，可得x-y=1；
当x≤0，y≥0时，可得-x+y=1．
图象如下图正方形ABCD．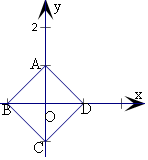

点评 本题考查方程表示的曲线，注意等价变形，考查数形结合思想方法，属于基础题．