
已知 ,函数
,函数 (
(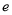 为自然对数的底数).
为自然对数的底数).
(Ⅰ)若 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅱ)若 的最小值为
的最小值为 ,求
,求 的最小值.
的最小值.
(Ⅰ) 的单调减区间为
的单调减区间为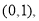 单调增区间为
单调增区间为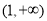 ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)由于当a=1时, ,则
,则 ,分别由f′(x)>0,f′(x)<0,进而求出函数f(x)的单调区间.
,分别由f′(x)>0,f′(x)<0,进而求出函数f(x)的单调区间.
(Ⅱ)由题意可知: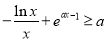 恒成立,且等号可取.令
恒成立,且等号可取.令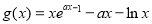 转化为方程
转化为方程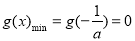 求解.
求解.
试题解析:(Ⅰ)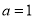 时,
时, ,
,
当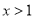 时,
时,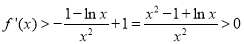
当 时,
时,
所以 的单调减区间为
的单调减区间为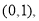 单调增区间为
单调增区间为 .
.
(Ⅱ)由题意可知: 恒成立,且等号可取.
恒成立,且等号可取.
即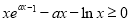 恒成立,且等号可取.
恒成立,且等号可取.
令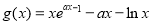
故 
由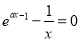 得到
得到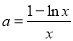 ,设
,设 ,
,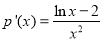
当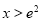 时,
时, ;当
;当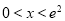 时,
时,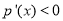 .
.
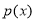 在
在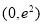 上递减,
上递减,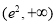 上递增.所以
上递增.所以
当 时,
时, 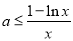 ,即
,即 ,
,
在 上,
上,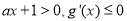 ,
,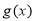 递减;
递减;
在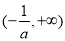 上,
上,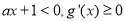 ,
,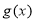 递增.
递增.
所以
设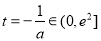 ,
,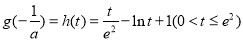
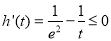 ,
,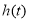 在
在 上递减,所以
上递减,所以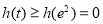
故方程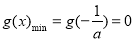 有唯一解
有唯一解 ,即
,即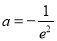 .
.
综上所述,当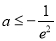 时,仅有
时,仅有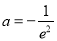 满足
满足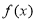 的最小值为
的最小值为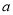 ,
,
故 的最小值为
的最小值为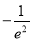 .
.
考点:1.利用导数研究函数的单调性;2.利用导数求函数的极值、最值;3.分类讨论.


科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=8,AC=7,BC=6,D是AB的中点,∠ADE=∠ACB,则DE= _________ .

查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:选择题
用反证法证明命题“若 a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
A.a,b都能被3整除 B.a不能被3整除
C.a,b不都能被3整除 D.a,b都不能被3整除
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株为样本,统计结果如下:
| 高茎 | 矮茎 | 合计 |
圆粒 | 11 | 19 | 30 |
皱粒 | 13 | 7 | 20 |
合计 | 24 | 26 | 50 |
(1)现采用分层抽样方法,从这个样本中取出10株玉米,再从这10株玉米中随机选出3株,求选到的3株之中既有圆粒玉米又有皱粒玉米的概率;
(2)根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考):
P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
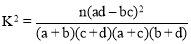 ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.
查看答案和解析>>
科目:高中数学 来源:2015届广东省梅州市高二下学期期中文科数学试卷(解析版) 题型:填空题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,给定下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本点的中心( ,
, );
);
③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com