
 已知菱形ABCD,AB=2,∠BAD=$\frac{π}{3}$,半圆O所在平面垂直于平面ABCD,点P在半圆弧上.(不同于B,C).
已知菱形ABCD,AB=2,∠BAD=$\frac{π}{3}$,半圆O所在平面垂直于平面ABCD,点P在半圆弧上.(不同于B,C).分析 (1)过O作OM⊥BC,连接OD,则BC⊥平面ABCD,OD⊥BC.以O为原点建立坐标系,则$\overrightarrow{OM}$为平面ABCD的法向量,设∠COP=θ,求出$\overrightarrow{AP}$的坐标,令|cos<$\overrightarrow{OM},\overrightarrow{AP}$>|=$\frac{\sqrt{2}}{4}$解出θ即可确定P点位置;
(2)令$\overrightarrow{PC}•\overrightarrow{BD}$=0解出θ,根据θ的范围得出结论.
解答 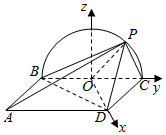 解(1)P为圆弧中点或者靠近点B的三等分点.
解(1)P为圆弧中点或者靠近点B的三等分点.
连接OD,在半圆内作OM⊥BC交圆弧于点M,则M为圆弧中点.
∵平面BCP⊥平面ABCD,平面BCP∩平面ABCD=BC,BC⊥OM,
∴OM⊥平面ABCD,
∵四边形ABCD是菱形,∠BAD=$\frac{π}{3}$,
∴△BCD是等边三角形,
∴OD⊥BC,于是OD,OC,OM两两垂直.
以O为原点,OD,OC,OM所在直线分别为x,y,z轴建立空间直角坐标系,
设∠COP=θ,θ∈(0,π),则P(0,cosθ,sinθ),A($\sqrt{3}$,-2,0),∴$\overrightarrow{AP}$=(-$\sqrt{3}$,cosθ+2,sinθ),
∵OM⊥平面ABCD,∴$\overrightarrow n=(0,0,1)$为平面ABCD的一个法向量,
∴cos<$\overrightarrow{AP},\overrightarrow{n}$>=$\frac{\overrightarrow{AP}•\overrightarrow{n}}{|\overrightarrow{AP}||\overrightarrow{n}|}$=$\frac{sinθ}{\sqrt{3+(cosθ+2)^{2}+si{n}^{2}θ}}$=$\frac{sinθ}{\sqrt{8+4cosθ}}$=$\frac{\sqrt{2}}{4}$.
解得$cosθ=0,或cosθ=-\frac{1}{2}$
∴$θ=\frac{π}{2},或θ=\frac{2π}{3}$
P为圆弧中点或者靠近点B的三等分点.
(2)假设存在点P使得PC⊥BD,设∠COP=θ.
∴P(0,cosθ,sinθ),C(0,1,0),B(0,-1,0),$D(\sqrt{3},0,0)$,
∴$\overrightarrow{BD}=(\sqrt{3},1,0)$,$\overrightarrow{CP}=(0,cosθ-1,sinθ)$
∵PC⊥BD,∴$\overrightarrow{BD}•\overrightarrow{CP}=0+cosθ-1+0=0$,
解得cosθ=1,则与θ∈(0,π)矛盾,
∴在半圆弧上不存在这样的点P使得PC⊥BD.
点评 本题考查了空间向量的应用,线面角的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
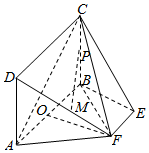 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
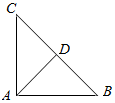 如图△ABC是直角边等于4的等腰直角三角形,D是斜边BC的中点,$\overrightarrow{AM}$=$\frac{1}{4}\overrightarrow{AB}$+m•$\overrightarrow{AC}$,向量$\overrightarrow{AM}$的终点M在△ACD的内部(不含边界),则实数m的取值范围是($\frac{1}{4}$,$\frac{3}{4}$).
如图△ABC是直角边等于4的等腰直角三角形,D是斜边BC的中点,$\overrightarrow{AM}$=$\frac{1}{4}\overrightarrow{AB}$+m•$\overrightarrow{AC}$,向量$\overrightarrow{AM}$的终点M在△ACD的内部(不含边界),则实数m的取值范围是($\frac{1}{4}$,$\frac{3}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y=0 | B. | x+y=0 | C. | x-y-2=0 | D. | x+y-2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com