
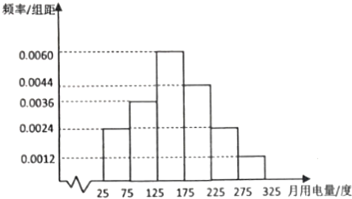
���� ��1����Ƶ�ʷֲ�ֱ��ͼ�ܹ��Ƹ��û������õ�����ƽ��ֵ��
��2����25��X��200ʱ��T=0.5X����200��X��325ʱ��T=200��0.5+��X-200����0.6=100+0.6��X-200�����ɴ�����������
��3��T��[37.5��115]���Ӷ�X��[75��225]���ɴ�����������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ���Ƹ��û������õ�����ƽ��ֵΪ��
$\overline{x}$=50��0.12+100��0.18+150��0.3+200��0.22+250��0.12+300��0.06=161���ȣ���
��2��ÿ���õ�����200�����ڣ���200�ȣ�����ÿ�ȵ��0.5Ԫ��
��ÿ�µ��õ�������200�ȣ����IJ���ÿ�ȵ��0.6Ԫ��
��X����λ���ȣ�25��X��325��Ϊ���û��¸��µ��õ�����T����λ��Ԫ��Ϊ�¸��������ɵĵ�ѣ�
�൱25��X��200ʱ��T=0.5X��
��200��X��325ʱ��T=200��0.5+��X-200����0.6=100+0.6��X-200����
��T=$\left\{\begin{array}{l}{0.5X��25��X��200}\\{100+0.6��X-200����200��X��325}\end{array}\right.$��
��3��T��[37.5��115]����X��[75��225]��
��P��T��[37.5��115����=P��X��[75.225����
=��0.0036+0.0060+0.0044����50=0.7��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{19}{32}$ | B�� | $\frac{9}{16}$ | C�� | $\frac{5}{8}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12$\sqrt{2}$ | B�� | 12 | C�� | 14 | D�� | 14$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
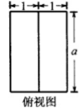 ��֪��������ABCD-A1B1C1D1�������������Σ����ⴹֱ�ڵ��棩��8�����㶼����O�ı����ϣ�AB=1��AA1��=2������O�İ뾶R=6�У���E��F����AA1��DD1���е㣬��ֱ��EF����O�صõ��߶γ�Ϊ$\sqrt{5}$��
��֪��������ABCD-A1B1C1D1�������������Σ����ⴹֱ�ڵ��棩��8�����㶼����O�ı����ϣ�AB=1��AA1��=2������O�İ뾶R=6�У���E��F����AA1��DD1���е㣬��ֱ��EF����O�صõ��߶γ�Ϊ$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | [1��2�� | C�� | [0��2�� | D�� | ��0��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com