
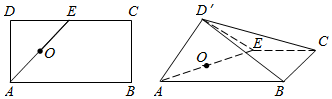
分析 (I)取BC中点F,连结OF,D′O,D′F,则BC⊥平面D′OF,于是BC⊥OD′,又OD′⊥AE,于是OD′⊥平面ABCE,故而平面D′AE⊥平面ABCE;
(II)以O为原点建立平面直角坐标系,求出平面ABD′的法向量$\overrightarrow{n}$,则CD′与平面ABD′所成角的正弦值等于|cos<$\overrightarrow{n}$,$\overrightarrow{CD′}$>|.
解答 解:(I取BC中点F,连结OF,D′O,D′F,则BC⊥OF,
∵D′B=D′C,∴BC⊥D′F
又∵OF?平面D′OF,D′F?平面D′OF,OF∩D′F=F,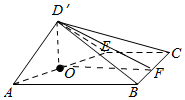
∴BC⊥平面D′OF,∵D′O?平面D′OF,
∴BC⊥D′O,
∵DA=DE,即D′A=D′E,
∴D′O⊥AE,又∵AE?平面ABCE,BC?平面ABCE,AE与BC相交,
∴D′O⊥平面ABCE,∵D′O?平面D′AE
∴平面D′AE⊥平面ABCE.
(II)以O为原点建立如图所示的空间直角坐标系O-xyz,
则A(1,-1,0),B(1,3,0),C(-1,3,0).D′(0,0,$\sqrt{2}$),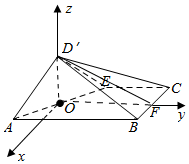
∴$\overrightarrow{D′A}$=(1,-1,-$\sqrt{2}$),$\overrightarrow{D′B}$=(1,3,-$\sqrt{2}$).$\overrightarrow{CD'}$=(-1,3,-$\sqrt{2}$).
设平面ABD′的法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{n}⊥\overrightarrow{D'A}$,$\overrightarrow{n}⊥\overrightarrow{D'B}$.
∴$\left\{\begin{array}{l}{x-y-\sqrt{2}z=0}\\{x+3y-\sqrt{2}z=0}\end{array}\right.$,令z=$\sqrt{2}$,得x=2,y=0,
∴$\overrightarrow{n}$=(2,0,$\sqrt{2}$).|$\overrightarrow{n}$|=$\sqrt{6}$,|$\overrightarrow{CD′}$|=2$\sqrt{3}$.$\overrightarrow{n}•\overrightarrow{CD′}$=-4.
∴cos<$\overrightarrow{n}$,$\overrightarrow{CD′}$>=$\frac{\overrightarrow{n}•\overrightarrow{CD′}}{|\overrightarrow{n}||\overrightarrow{CD′}|}$=-$\frac{\sqrt{2}}{3}$.
∴CD′与平面ABD′所成角的正弦值为$\frac{\sqrt{2}}{3}$.
点评 本题考查了面面垂直的判定,线面角的求解方法,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一次文、理科学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩X,文综成绩为Y,|X-Y|为Z,将Z值分组统计制成下表,并将其中女生的Z值分布情况制成频率分布直方图
在一次文、理科学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩X,文综成绩为Y,|X-Y|为Z,将Z值分组统计制成下表,并将其中女生的Z值分布情况制成频率分布直方图| 分组 | [0,20) | [20,40) | [40,60} | [60,80) | [80,100) | [100,120) | [120,140) |
| 频数 | 4 | 18 | 42 | 66 | 48 | 20 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
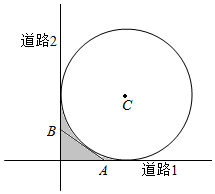 如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤1} | B. | {x|0≤x≤1} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
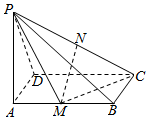 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com