
���� ��1�����ݹ�F1��ֱ�߽���Բ��A��B���㣬�ҡ�ABF2���ܳ�Ϊ12���ɵ�4a=12����a=3������e=$\frac{1}{3}$��b2=a2-c2=8�����������ԲE�ķ��̣�
��2����$\left\{\begin{array}{l}{y=kx+m}\\{8{x}^{2}+9{y}^{2}=72}\end{array}\right.$����Ԫ�ɵã�9k2+8��x2+18kmx+9m2-72=0�����ö�ֱ��l��y=kx+m����ԲE����ֻ��һ��������P��x0��y0�����ɵ�m��0����=0�������ɵ�P�����꣬��$\left\{\begin{array}{l}{y=kx+m}\\{x=9}\end{array}\right.$���ɵ�Q�����꣬ȡk=0��m=2$\sqrt{2}$��k=-$\frac{1}{3}$��m=3���������������ĵ�M���ڣ�ֻ����M��1��0��������������ֱ������֤�����ɣ�
��� 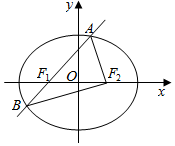 �⣺��1����F1��ֱ�߽���Բ��A��B���㣬�ҡ�ABF2���ܳ�Ϊ12��
�⣺��1����F1��ֱ�߽���Բ��A��B���㣬�ҡ�ABF2���ܳ�Ϊ12��
����Բ�Ķ���ɵ�AF1+AF2=BF1+BF2=2a��
���С�ABF2���ܳ�Ϊ4a=12���ɵ�a=3��
��e=$\frac{c}{a}$=$\frac{1}{3}$���ɵ�c=1��
����b2=a2-c2=8��
����ԲE�ķ���Ϊ$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1��
��2����$\left\{\begin{array}{l}{y=kx+m}\\{8{x}^{2}+9{y}^{2}=72}\end{array}\right.$����y�ɵã�9k2+8��x2+18kmx+9m2-72=0��
�ɶ�ֱ��l��y=kx+m����ԲE����ֻ��һ��������P��x0��y0����
�ɵ�m��0����=0����Ϊ��18km��2-4����9k2+8������9m2-72��=0��
��Ϊ9k2-m2+8=0��
��ʱx0=-$\frac{9km}{9{k}^{2}+8}$=-$\frac{9k}{m}$��y0=$\frac{8}{m}$��
��P��-$\frac{9k}{m}$��$\frac{8}{m}$��
��$\left\{\begin{array}{l}{y=kx+m}\\{x=9}\end{array}\right.$����Q��9��9k+m����
ȡk=0��m=2$\sqrt{2}$����ʱP��0��2$\sqrt{2}$����Q��9��2$\sqrt{2}$����
��PQΪֱ����ԲΪ��x-$\frac{9}{2}$��2+��y-2$\sqrt{2}$��2=$\frac{81}{4}$��
��x���ڵ�M1��1��0����M2��8��0��
ȡk=-$\frac{1}{3}$��m=3����ʱP��1��$\frac{8}{3}$����Q��9��0����
��PQΪֱ����ԲΪ��x-5��2+��y-$\frac{4}{3}$��2=$\frac{160}{9}$��
��x���ڵ�M3��1��0����M4��9��0����
�������������ĵ�M���ڣ�ֻ����M��1��0����֤������
��$\overrightarrow{MP}$=��-$\frac{9k}{m}$-1��$\frac{8}{m}$����$\overrightarrow{MQ}$=��8��9k+m����
�ɵ�$\overrightarrow{MP}$•$\overrightarrow{MQ}$=8��-$\frac{9k}{m}$-1��+$\frac{8}{m}$��9k+m��=0��
����PQΪֱ����Բ���x���ϵĶ���M��1��0����
���� ������Ҫ���������ߵĶ��������ʡ�Բ��ֱ�����Ե�Բ�ܽ�Ϊֱ�ǡ�ֱ������Բ��λ�ù�ϵ�������������������黯��˼�룬�����е��⣮


 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 4 | C�� | -1 | D�� | $\frac{16}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | $\sqrt{5}$ | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 2 | C�� | $\sqrt{5}$ | D�� | $2\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?�ա�R������f��x��=sin��2x+�գ�������ż���� | |
| B�� | ?�����¡�R��ʹcos����+�£�=cos��+cos�� | |
| C�� | ����$\overrightarrow a$=��-2��1����$\overrightarrow b$=��-3��0������$\overrightarrow a$��$\overrightarrow b$�����ϵ�ͶӰΪ2 | |
| D�� | ��|x|��1���ǡ�x��1���ļȲ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-2��2+y2=$\sqrt{10}$ | B�� | ��x+2��2+y2=10 | C�� | ��x+2��2+y2=$\sqrt{10}$ | D�� | ��x-2��2+y2=10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 7 | C�� | 6 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com