
分析 利用分析法和基本不等式性质证明.
解答 证明:要证$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$≤$\sqrt{3}$,
只需证($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2≤3,展开得a+b+c+2($\sqrt{ab}$+$\sqrt{bc}$+$\sqrt{ca}$)≤3,
又因为a+b+c=1,
所以即证$\sqrt{ab}$+$\sqrt{bc}$+$\sqrt{ca}$≤1.
因为a,b,c为非负实数,
所以$\sqrt{ab}$≤$\frac{a+b}{2}$,$\sqrt{bc}$≤$\frac{b+c}{2}$,$\sqrt{ca}$≤$\frac{c+a}{2}$.
三式相加得$\sqrt{ab}$+$\sqrt{bc}$+$\sqrt{ca}$≤$\frac{2(a+b+c)}{2}$=1,
所以$\sqrt{ab}$+$\sqrt{bc}$+$\sqrt{ca}$≤1成立.
所以$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$≤3.
点评 本题考查了不等式的证明,掌握不等式的性质和证明方法是关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
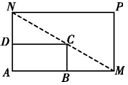 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,a:b:c=sinA:sinB:sinC | |
| B. | 在△ABC中,若sin2A=sin2B,则a=b | |
| C. | 在△ABC中,若sinA>sinB,则A>B,若A>B,则sinA>sinB | |
| D. | 在△ABC中,$\frac{a}{sinA}=\frac{b+c}{sinB+sinC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com