
| ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ��ѧ�ɼ���x/�֣� | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
| ��һ��ĩ�ɼ���y/�֣� | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
���� ��1�������������ݻ���ɢ��ͼ��
��2���Ա���x��y��������Լ��飬���x��y֮�����������ع�ϵ�����b��a����������ع�ֱ�߷��̣�
��3�����ûع�ֱ�߷��̹������ڸ�һ��ĩ�����е���ѧ�ɼ���
��� �⣺��1 ������ѧ�ɼ�xΪ�Ա�������ĩ�ɼ�yΪ���������ɢ��ͼ��ͼ��
���Կ���������������бȽϺõ�������ع�ϵ��
��2����Ϊ$\overline{x}$=70��$\overline{y}$=76��$\sum_{i=1}^{10}$��xi-$\overline{x}$����yi-$\overline{y}$��=1894��$\sum_{i=1}^{10}$��xi-$\overline{x}$��2=2474
��b��0.7656��a=22.408��
�����������Իع鷽����y=0.7656x+22.408��
��3����ijѧ����ѧ��ѧ�ɼ�Ϊ80�֣�
����ع鷽�̿����y��84��
�����ѧ����һ��ĩ��ѧ�ɼ���Ԥ��ֵΪ84�֣�
���� ���⿼�����Իع鷽�̣�����ѧ���ļ��������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0 | C�� | -1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=ax2+bx+c��a��0����ͼ���ԭ�㣬����x����A��-6��0���������ߵĶ���B��������Ϊ-$\sqrt{3}$��
��ͼ����֪������y=ax2+bx+c��a��0����ͼ���ԭ�㣬����x����A��-6��0���������ߵĶ���B��������Ϊ-$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
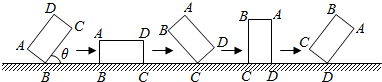
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����f��x��=|x-1|+|x+1|��x��R��
��֪����f��x��=|x-1|+|x+1|��x��R���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com